3. Math of House Buying
by M. Bourne
Disclaimer
This discussion is simplified so we don’t get lost in complications. Also, interest rates are changing all the time - check your local banks for latest rates.
There is no need to really use the formulas in this section. You can easily use Excel to calculate the values or you can use the many on-line calculators to find the values.
This site does not contain investment advice.
Don’t miss interactive mortgage calculators on this page.
Tom (see the chapter intro) wants to buy a house sometime soon. He knows that real estate is a reasonably safe way to build wealth. It is slow, but generally low risk.

He will come across a bewildering choice of mortgages. A mortgage is just a fancy word for the process of borrowing money for a house.
The bank actually buys the house and keeps the title deed. You agree to pay off the borrowed amount each month, usually over a period of 20 to 30 years. When you have finally paid it off, you get the title deed, meaning you now fully own the house.
If you stop paying for any reason, the bank has the right to sell the house. After all, they own most of it.
Mortgage Example
Tom’s house will cost `$300,000`. He needs to pay a deposit of `10%` and will pay the remaining `90%` over `30` years at `8%` per annum.
So he will need to pay a deposit of `10%` of `300,000 = $30,000`.
The remaining amount he owes is `$270,000`.
Monthly Payments
The formula for the amount Tom has to pay each month is
`A=(Lxxr)/(1-(1+r)^-n)`
where
A = amount to pay each month
L = loan amount (or principal)
r = interest rate (per year as a decimal - or divide by `12` to get the rate per month)
n = number of payments
(This formula is based on the Sum of a Geometric Progression.)
So for our case, we have:
`L = 270,000`
`r = 8% -: 12 = 0.0066667`
`n = 30 xx 12 = 360`
So the amount is
`text(Payment)=(Lxxr)/(1-(1+r)^-n)`
`=(270000xx0.08/12)/(1-(1+0.08/12)^-360)`
`=$1981.16`
So Tom needs to find just under $2000 per month to buy his house. Of course, he won’t be paying rent so the extra amount is not too bad, he figures.
Back of the Envelope Calculation
A reader asked if there is a reasonable approximation that we can use for this formula when we want to do "back of the envelope" calculations. It turns out there is.
("Back of the envelope" is an expression meaning we can work it out quickly and easily on a scrap of paper.)
Most mortgages are for less than 30 years. The following chart illustrates the value of the denominator for the above expression, for interest rates of `6%` to `14%` up to 30 years.
For example, the graph for lowest curve, `6%`, is of the following form, where n is the number of years:
`1 - (1 + 0.06/12)^(12n)`
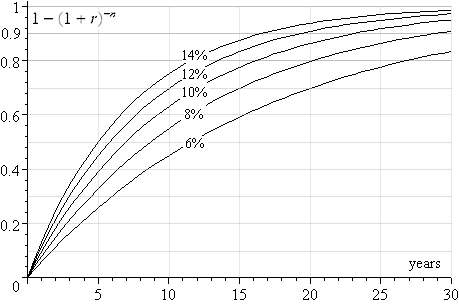
We can use this graph as follows.
If the mortgage is `25` years and the interest rate is `10%`, the graph tells us the denominator value is close to `0.91`.
So a `$100,000` loan would have a monthly payment of about
`(100,000xx0.1/12)/0.91=916`
A check in the actual formula yields a value of `$908.70`. So the approximation is not bad.
Interest amount in each payment
The formula for the amount of interest we pay in each installment is:
`"Interest"` `=(Lxxr(1-(1+r)^(p-n)))/(1-(1+r)^-n)`
Considering the example given above, in the first month of our mortgage repayments, we pay in interest:
`(170000xx0.0066667(1-(1+0.006667)^(1-360)))/(1-(1+0.006667)^-360)` `= 1798.79`
So early in the repayments, we pay a large amount off the interest (and very little off the principle: `{:1981.16 - 1798.79 = 182.37).`
Later in the process, say at the 25-year point (the 300th payment), the amount of interest we pay that month is:
`(170000xx0.0066667(1-(1+0.006667)^(300-360)))/(1-(1+0.006667)^-360)` `= 651.39`
We are now paying much less interest, and a lot more off the principle: `1981.16 - 651.39 = 1329.77.`
Interactive Mortgage Payments Calculator
You can calculate any repayment here. Change any of the values for principal, interest or period and then click "Calculate". You can also see a graph of the equity (the amount you own) that has been built up in the property over time.
If you move your cursor over any of the graph bars that appear, a tooltip will tell you how much is still owing, and how much equity you have in the house.
The amounts show are for the beginning of the year in each case, so at the beginning of Year 1, you owe the full amount and have no equity, while at the beginning of Year 31 (in the example given), you have paid it all off and now you own the house outright.
NOTE: This interactive assumes zero house price inflation. If you are lucky, your house will increase in value and will be worth more than you paid for it. But that doesn't always happen.
Principal = $ (min 50000, max 10 million)
Interest p.a. = % (min 0.01, max 100)
Period = years (min 5, max 35)
Year
Copyright © 2013 www.intmath.com
Note: These calculations do not take into account the bank fees and we are assuming a fixed rate of interest for the whole period of the loan. Actual amounts charged by lenders are sure to be higher than this.
Six Months Later
Tom has been paying off his pride and joy for 6 months. He has paid a total of `$1981.16 xx 6` ` = $11886.96`.
He gets the first statement from the bank and expects to see a reasonable dent in the amount he owes. He is shocked to find that he still owes `$268,894.74`. How is this possible? He has paid `$12000` but only around `$1000` has come off the balance.
The formula for the balance is:
`text(Balance)=(L[1-(1+r)^(p-n)])/(1-(1+r)^-n)`
where
L = the loan amount
r = interest rate per month as a decimal
p = number of payments already made
n = total number of payments to be made
In our example, the balance will be:
`text(Balance)=(L[1-(1+r)^(p-n)])/(1-(1+r)^-n)`
`=(270000[1-(1+0.08/12)^(6-360)])/(1-(1+0.08/12)^-360)`
`=$268\ 894.74`
With mortgages, the amount you are paying early in the loan period is mostly interest, and very little is coming off the principal. Towards the end of the loan, the interest amount is less and the principal starts to disappear more quickly.
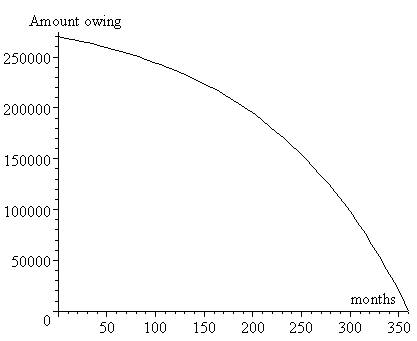
Amount ($) still owing after p months.
The mistake a lot of people make is to sell the house quickly. The average mortgage is only 7 years. They own very little of the house by then because they have mostly been paying interest to the bank. If house prices have gone up a lot, they are ahead. But if house prices level off, or decline, then they lose a lot of money.
Reader Question
Reader David asked:
Is it possible to derive an equation for when the interest part of the payment for a loan exactly equals the principal part of the payment?
There is, David, and here's how to do it.
Answer
This question has two related parts — when the amount of interest in the payment is equal to the equity amount in the payment; and when the total amount of interest paid equals the total amount of principle paid. They are around the same time, but not exactly.
Interest payment equals principle payment
To calculate this, we need to determine when the:
interest paid in month p = 0.5 × monthly payment
That is, when:
`(Lr(1-(1+r)^(p-n)))/(1-(1+r)^-n)` ` = 0.5xx(Lr)/(1-(1+r)^-n)`
Simplifying this (by multiplying throughout by `(1-(1+r)^-n)` and dividing by `Lr` gives:
`1-(1+r)^(p-n) = 0.5`
`(1+r)^(p-n) = 0.5`
Using our example from before, with:
L = 270000
r = 0.08/12 = 0.0066667
p = unknown
n = 360
We only need `r` and `n`, so we substitute:
`(1+0.00666667)^(p-360) = 0.5`
Taking log of both sides:
`(p-360)log(1+0.00666667) ` `= log(0.5)`
Solving for `p`:
`p ` `= (log(0.5))/log(1+0.00666667) + 360` `~~256`
So the month where the amount paid in interest and the amount paid in principle is (very close to) the same, is the 256th month.
Total Interest paid equals Total Principle paid
The interest part of the total amount paid so far will equal the principal paid so far when the the balance owing equals the equity (the amount of the house we own).
We saw earlier that:
`text(Balance)=(L[1-(1+r)^(p-n)])/(1-(1+r)^-n)`
The amount of equity we have in the house is simply the house value minus what we still owe. So:
`text(Equity)=L - (L[1-(1+r)^(p-n)])/(1-(1+r)^-n)`
Setting these equal gives:
`(L[1-(1+r)^(p-n)])/(1-(1+r)^-n)` `=L - (L[1-(1+r)^(p-n)])/(1-(1+r)^-n)`
We need to solve for `p`, the number of payments already made.
Multiplying throughout by `1-(1+r)^-n` gives:
`L[1-(1+r)^(p-n)]` `=L[1-(1+r)^-n]` ` - L[1-(1+r)^(p-n)]`
Adding `L[1-(1+r)^(p-n)]` to both sides then cancelling the `L`'s gives:
`2[1-(1+r)^(p-n)]` `=[1-(1+r)^-n]`
Rewriting:
`2[1 - ((1+r)^p)/(1+r)^n] =1-1/((1+r)^n)`
Multiplying throughout by `(1+r)^n` gives:
`2[(1+r)^n - (1+r)^p]` ` =(1+r)^n - 1`
`(1+r)^n - 2(1+r)^p = - 1`
Tidying this up and getting the `(1+r)^p` term on the left hand side:
`(1+r)^p = 0.5[(1+r)^n+1]`
Taking log of both sides:
`log(1+r)^p = log[0.5((1+r)^n+1)]`
This is equivalent to:
`p log(1+r) = log[0.5((1+r)^n+1)]`
So
`p = (log[0.5((1+r)^n+1)])/log(1+r)`
In the example given earlier on this page, we had:
L = 270000
r = 0.08/12 = 0.0066667
p = unknown
n = 360
Therefore, the required time is:
`p = (log[0.5((1+0.08/12)^360+1)])/log(1+0.08/12)` ` = 280.959 ~~ 281`
This means the principal equals the equity on the 281st payment, i.e. the 4th payment of the 23rd year.
Money Maths Lesson Plan Suggestion - House Buying
Simulate a house buying scenario in your district. Use actual advertisements for houses and for housing loans. Get students to find the best loan deals. Which is best - fixed or variable interest? What will they pay in total for the house? What will it be worth at the end of the loan period? How much will they have paid after 10 years and how much will they own by then?
Footnote
It may not always be best to buy a house compared to renting. In Japan, house prices have still not recovered to where they were 16 years ago. Sure, interest rates are low there, but negative equity has been a huge problem for years. (This is when the amount that you owe on a house is more than what the house is worth.)
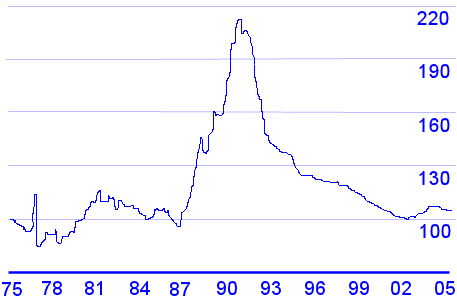
House prices, Japan. Index = 100 in 1975.
This means that house prices more than doubled at the peak in 1991 and have dropped back to 1975 levels since. In 2005/2006 there has been a modest increase.
Interestingly, house prices in US, Australia, UK, and most industrialised economies have shot up in recent years due to low interest rates. One wonders what the future holds for house prices in these countries...
If rents are low in your area, it may be better to rent a place and invest (not spend) the difference.