Skip to main content
Interactive Mathematics
Search IntMath
Close

Home | Math art in code | CSS Matrix - a mathematical explanation

Page by Murray Bourne, IntMath.com. Last updated: 07 Sep 2019

CSS Matrix - a mathematical explanation

This article gives an overview of CSS transforms, and explains how they can be replaced using a single transform with CSS matrix. It shows where the numbers come from in CSS matrix, the result of matrix multiplication.

CSS matrix - a mathematical explanation

CSS transform basics

On this page...

CSS transform basics

Transform-origin

CSS transform examples

Order of transforms

CSS matrix elements

Combined CSS transforms

Writing the transform using a matrix

Explanation via matrix multiplication

Easy ways to calculate CSS matrix

Matrices and SVG

Further resources

A transform is a change in the shape or size of an object. We can scale the object (changing the size), skew it ("squashing" the object), rotate it, or translate it (moving left-right, or up down).

On Web pages, we can change the colors, font-sizes, shapes and all sorts of other characteristics using CSS (cascading style sheets). This article will concentrate on transformations, and in particular, the matrix transform.

CSS matrix tranform

To change the shape or size of an object, we apply some CSS transforms. The browser (in the background) converts those transforms into a matrix, something like this:

transform: matrix(2.0945, 0.4937, 0.2679, 1.4, 150, 50)

I wanted to know more about how this transform matrix worked. Specifically, I wanted to know:

  1. Where do those numbers come from?
  2. What do the numbers signify?
  3. How are they applied to objects in order to change their size, shape and position?

Incomplete and inaccurate information

I make use of matrices when transforming SVG (and occasionally HTML objects), but I found myself often confused about what the numbers in the matrix actually represent, so when I went to manipulate them, it tended to be trial and error. Not good.

So I decided I needed to find out more about them.

I started with the (usually excellent) MDN's matrix page, but found it very disappointing in this case. It didn't answer my main questions, and in fact didn't give me much useful information at all.

So I went looking for other resources, where I found statements like "the browser works out the matrix for you, so you don't need to worry about it". But I was on a quest, and this was no help. I also found some quite misleading information, but more on that later.

Important gotcha - transform-origin

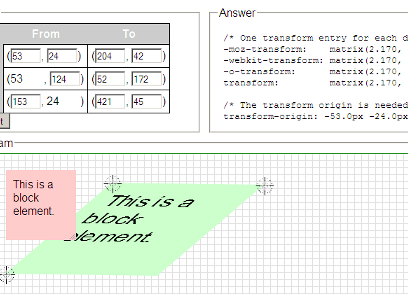
Before talking about transforms and matrices, we'll briefly describe the important concept of transform-origin – this is something that can easily bite you in the tail. It's quite possible to have an object disappear right off the screen when performing a simple transform, and often the culprit is the origin of the transform has not been set, or has been set differently to what you expect.

For each of these examples, we're going to rotate the image (clockwise) by 20o. However, they all have different transform-origins.

Click on each picture to see how the transform is different for different transform-origins.

transform:rotate(20deg)

The browser default is transform-origin:50% 50%, and it means the image will rotate around its center, while "transform-origin:0 0" means it will rotate around the top left of the picture.

Default

Gotcha

transform-origin:0 0

Gotcha

"100% 100%" means the image will rotate around its bottom right corner, while I set "126px 52px" so it rotates around a key focus of the image.

transform-origin:100% 100%

Gotcha

transform-origin:126px 52px

Gotcha

For the rest of the examples on this page, the transform-origin is set to 0 0 (top left).

CSS transform examples

Before we see what CSS matrix can do for us, here's a quick reminder of some of the main transforms, and how we achieve them using CSS.

We start with an immortal quote by Morpheus from The Matrix. It's contained in a <div> with a border. We're going to perform six transforms on this <div>.

Original div

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

First we apply scaleX(2) which stretches the whole thing by 2 in the x-direction; then in (b) we start again and this time skew it in the y-direction by 10o.

You can see the (greyed out) original <div> underneath, for comparison.

(a) transform: scaleX(2)

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

(b) transform: skewY(10deg)

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

Next, we'll skew the original <div> in the x-direction by 15o and then start over in (d) and scale it by 1.4 in the y-direction.

We're doing these in a strange order and I hope the reason for it will become clear soon.

(c) transform: skewX(15deg)

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

(d) transform: scaleY(1.4)

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

Finally, we translate (simply move) the <div> in the x-direction by 150 px and then by 50 px in the y-direction (positive is down for CSS transforms.)

(e) transform: translateX(150px)

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

(f) transform: translateY(50px)

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

Does the order of transforms matter?

Observe the following two examples. In the first one, (g), we rotate the <div> first, then we scale it in the x-direction. Notice the sides of the transformed <div> do not meet at right angles.

In the second one, (h), the scaleX(0.6) happens first, and then the rotation. This time, the sides meet at right angles, and the transformed <div> is "skinny".

(g) transform: scaleX(0.6) rotate(-120deg)

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

(h) transform: rotate(-120deg) scaleX(0.6)

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

So the order of transforms does matter. (In mathematical language, we say they are not commutative.) We'll see soon that this is because matrix multiplication is generally not commutative, and these transforms are the result of (internal) matrix multiplications.

CSS Matrix elements

The CSS transform matrix consists of 6 numbers, as mentioned earlier.

Some resources (like Quackit's CSS matrix() Function) give the misleading information that the numbers in a transform matrix are as follows:

matrix(
scaleX,
skewY,
skewX,
scaleY,
transX,
transY
)

However, this only applies if we are doing one transform at a time.

Before showing how this is misleading, let's go through some simple matrix examples first.

The "unit" transform matrix

A transform matrix that does not change the shape, size or position in any way would be written as:

transform: matrix(1, 0, 0, 1, 0, 0)

The numbers in the scaleX and scaleY positions are both 1 (we are not changing the size), and skewY and skewX are 0 (we are not skewing the object at all), and finally, translateX and translateY are 0, so we are not moving the object anywhere.

Writing single transforms using CSS matrix

The first transform we did, scaleX(2) can be written as:

transform: matrix(2, 0, 0, 1, 0, 0)

Similarly, the second transform we did, skewY(10o) can be written as (matrix uses the tan of the angle):

transform: matrix(1, 0.1745, 0, 1, 0, 0)

The third transform we did, skewX(15o) can be written as (once again, matrix uses the tan of the angle):

transform: matrix(1, 0, 0.2618, 1, 0, 0)

The fourth transform we did, scaleY(1.4) can be written as:

transform: matrix(1, 0, 0, 1.4, 0, 0)

The fifth transform we did, translateX(150px) can be written (without the px units) as:

transform: matrix(1, 0, 0, 1, 150, 0)

The last transform we did, translateY(50px) can be written (without the px units) as:

transform: matrix(1, 0, 0, 1, 0, 50)

Notice we are doing one transform only in each case.

What if we want to apply all of the transforms together?

Earlier. we applied 6 different transforms, one after the other (in examples (a) to (f)), in this order:

scaleX(2), skewY(10deg), skewX(15deg), scaleY(1.4), translateX(150px), translateY(50px)

If we want the browser to apply all 6 transforms, in that order but all at once, we need to present them in our CSS in REVERSE order (since the browser applies them in the order right to left), like this:

transform: translateY(50px) translateX(150px) scaleY(1.4) skewX(15deg) skewY(10deg) scaleX(2)

Combined CSS transforms

Here's the result of applying all 6 transforms "at once".

(i) transform: translateY(50px) translateX(150px) scaleY(1.4) skewX(15deg) skewY(10deg) scaleX(2)

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

Simplifying, using CSS matrix

The browser first converts such a combined transform into a single matrix expression. (In fact, it does this for all transforms.) Let's see how this works.

Need revision?

First, check these pages for some quick revision if you are rusty with matrix multiplication.

Matrix multiplication examples

Add, Subtract and Multiply matrices interactive

This next page has an interactive applet where you can explore the way matrix multiplication determines different transformations.

Matrices and Linear Transformations

Writing the transform using a matrix

This is what your browser does under the hood. Whenever you invoke one or more CSS transforms, the browser calculates the resulting position, size and shape via an internal series of matrix multiplications.

If you apply this transform (the one we've been using in examples above):

transform: translateY(50px) translateX(150px) scaleY(1.4) skewX(15deg) skewY(10deg) scaleX(2)

... the developer's console in your browser indicates the following:

transform: matrix(2.0945, 0.4937, 0.2679, 1.4, 150, 50)

Where do those numbers come from?

My first attempt at working these out was as follows. Starting from the right end (since the transformations are applied from right to left), we have:

translateY(50px) is the final number (without px units);

translateX(150px) is the second last number (without px units);

scaleY(1.4) is the 4th number;

tan(15o) = 0.2679 is the 3rd number

scaleX*scaleY*tan(10o) = 0.4937 is the 2nd number

scaleX(2) + ??? = 2.0945

I worked out the first five above using some reasonable guesses, but I couldn't at first see why that last one wasn't 2 exactly, and where that 0.0945 came from.

Knowing that transforms "work" by a series of matrix multiplications, I then set up the appropriate transform matrices and multiplied them.

Explanation via matrix multiplication

We consider the last 4 transforms (the ones not involving translation) only for now (since they can be calculated using 2×2 matrices).

So this 4-item transform...

transform: scaleY(1.4) skewX(15deg) skewY(10deg) scaleX(2)

becomes the following when written using (mathematical) matrices...

`[(1,0),(0,1.4)]``[(1,tan(15^"o")),(0,1)]``[(1,0),(tan(10^"o"),1)]``[(2,0),(0,1)]`

(See Matrices and Linear Transformations referred to above to see where these matrices come from.)

When multiplying more than one matrix, we start with the right-most 2 matrices (the 2 magenta ones) and multiply those. (This is also why the browser applies transforms from right to left, of course.)

`=[(1,0),(0,1.4)]``[(1,tan(15^"o")),(0,1)]` `[(2,0),(2tan(10^"o"),1)]`

Next we multiply the second matrix (in blue) with the result of the last line:

`=[(1,0),(0,1.4)][(2+2tan(10^"o")tan(15^"o"),tan(15^"o")),(2tan(10^"o"),1)]`

Finally, we multiply the first matrix with the result of the last line:

`=[(2+2tan(10^"o")tan(15^"o"),tan(15^"o")),(2.8tan(10^"o"),1.4)]`

`=[(2.0945,0.2679),(0.4937,1.4)]`

So this means the 4-item transform transform: scaleY(1.4) skewX(15deg) skewY(10deg) scaleX(2) effectively becomes the above matrix.

Translation requires a 3×3 matrix

Our 2×2 matrix does not yet cater for translation. As we learned in Matrices and Linear Transformations, we need to use a 3×3 matrix for this.

Substituting what we've done so far into the top-left position of a 3×3 matrix:

`[(\color(#f0f)2.0945,\color(#00f)0.2679,"translateX"),(\color(#00f)0.4937,\color(#f0f)1.4,"translateY"),(0,0,1)]`

In our example translateX is 150 px and translateY is 50 px, so we'll have:

`[(\color(#f0f)2.0945,\color(#00f)0.2679,150),(\color(#00f)0.4937,\color(#f0f)1.4,50),(0,0,1)]`

The last row of our (mathematical) matrix is a "dummy" row that always has values 0, 0, 1.

Finally we now know where the numbers are coming from in a CSS matrix. Reading down the columns, we have:

transform: matrix(2.0945, 0.4937, 0.2679, 1.4, 150, 50)

Unit transform matrix

The mathematical way of writing a matrix that doesn't change the object in any way (a "unit transform matrix") is as follows:

`[(\color(#f0f)1,\color(#00f)0,0),(\color(#00f)0,\color(#f0f)1,0),(0,0,1)]`

Applying CSS matrix instead of separate transforms

After all that, we apply the matrix we've been discussing, and find the end result is indeed the same as transform (i), as expected.

(j) transform: matrix(2.0945, 0.4937, 0.2679, 1.4, 150, 50)

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

"This is your last chance. After this, there is no turning back."

—Morpheus

Morpheus

Writing CSS Matrices mathematically

The first transform we did, scaleX(2) can be written as:

transform: matrix(2, 0, 0, 1, 0, 0)

Writing it as a mathematical matrix, this is (remember the last row of our matrix is a "dummy" row that doesn't do anything, and we are going down each column of the first 2 rows):

`[(\color(#f0f)2,\color(#00f)0,0),(\color(#00f)0,\color(#f0f)1,0),(0,0,1)]`

Similarly, the second transform we did, skewY(10o) can be written as (we need to take the tan of that angle):

transform: matrix(1, 0.1763, 0, 1, 0, 0)

Writing it as a mathematical matrix, this is:

`[(\color(#f0f)1,\color(#00f)0,0),(\color(#00f)0.1763,\color(#f0f)1,0),(0,0,1)]`

The third transform we did, skewX(15o) can be written as (we need to take the tan of that angle):

transform: matrix(1, 0, 0.2679, 1, 0, 0)

Writing it as a mathematical matrix, this is:

`[(\color(#f0f)1,\color(#00f)0.2679,0),(\color(#00f)0,\color(#f0f)1,0),(0,0,1)]`

And so on. For each of these examples, we are doing one transform at a time.

What are the easiest ways to calculate CSS matrix?

Example: title slide

This was the title slide (reproduced from above) I used in a talk on this topic recently. The title text is made to look like it is actually on the billboard. To make it look realistic, I needed to apply a 3D transform.

CSS matrix - a mathematical explanation

3D-transform

So far in this article we've been discussing 2D transforms. When we apply such transforms to a rectangle, we end up with some kind of parallelogram. But the above bill board does not have any parallel sides, when viewed from this direction.

This was the matrix I used to line up the text appropriately:

matrix3d(
    1.8724, 0.6193, 0,  0.0009, 
   -0.2480, 1.3901, 0, -0.0005, 
     0,        0,   1,     0, 
    150,      50,   0,     1)

This is just an extension of the 2D matrices we've been talking about. The 3rd row and 3rd column are just "dummy" lines (they need to be there, but always have the values 0 or 1 as shown), the bottom left 2 numbers are x- and y-tanslations, and the two numbers in the top right corner are the result of multiplying 3D matrices.

In summary, a 2D transform uses a 3×3 matrix, while a 3D transform uses a 4×4 matrix.

I used the following tool to work out this 3D transform matrix.

Useful CSS matrix tools

Of course, we don't need to calculate such matrices as the browser does it for us "under the hood". However, there are times where we want to apply a matrix but don't know the exact scale, skew and so on.

Here are some tools that help in the process.

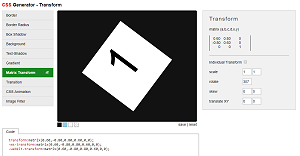
(1) The CSS3 Matrix Construction Set (by UserAgentMan)

screen shot

(2) CSS Generator - Transform (AngryTools)

This one is interesting but it makes no mention of the tangent ratio involved in the skew transformation, so it wasn't clear whether the slider was in degrees, radians or what. (It's not the angle, it's the result of taking the tan of an angle.)

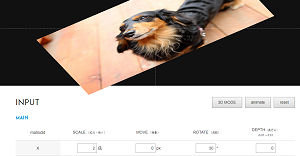
screen shot

(3) CSS Generator - Transform (ds-overdesign)

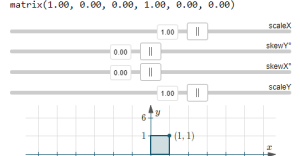
screen shot

CSS matrix interactive applet (IntMath)

This is my own, and I hope it's useful.

screen shot

Matrices and SVG

Matrix-based transforms work similarly to HTML CSS matrix transforms, except:

transform-origin: is at top-left of the element, not in the middle as in HTML, all except Firefox, that has it at middle (this has been an on and off "bug" since 2014).

SVG example using matrix transforms: Eigenvectors concepts

Further Resources

Understanding the CSS Transforms Matrix (Opera - one of the best)

The CSS3 matrix() Transform for the Mathematically Challenged (User Agent Man - quite good mathematical explanation)

An Introduction to CSS 3-D Transforms (David DeSandro - good examples)

CSS matrix() Function (Quackit - some misleading information)

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.