Differential equation: separable [Solved!]
Struggling 07 Feb 2017, 00:29
My question
Y=-3xdy/dx and y(1)= e
Relevant page
What I've done so far
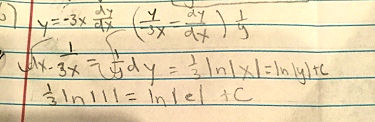
Struggling 07 Feb 2017, 00:29
Y=-3xdy/dx and y(1)= e
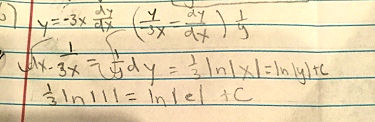
X
Y=-3xdy/dx and y(1)= e
Relevant page <a href="/differential-equations/2-separation-variables.php">2. Separation of Variables</a> What I've done so far
Murray 07 Feb 2017, 21:02
Hello, Struggling
First, be careful with upper- and lower-case variables - they mean different things.
I believe your question is actually `y=-3xdy/dx` and not `Y=-3xdy/dx.`
Also, you are encouraged to use the math entry system here - it's easier than uploading a photo!
In your second line, the negative is hard to read. I gather this is what you mean:
`int 1/(-3x) dx = int 1/y dy`
Also be careful with the "=" sign. The one in the middle of your second line is "dangerous", since the expression immediately to the left of it will not necessarily be equal to the one immediately to the right when solving DEs. (Here, it could be correct, if the negative wasn't dropped.) It's best to write a new line.
The last part of the second line has a problem. Where did the negative go?
X
Hello, Struggling First, be careful with upper- and lower-case variables - they mean different things. I believe your question is actually `y=-3xdy/dx` and not `Y=-3xdy/dx.` Also, you are encouraged to use the math entry system here - it's easier than uploading a photo! In your second line, the negative is hard to read. I gather this is what you mean: `int 1/(-3x) dx = int 1/y dy` Also be careful with the "=" sign. The one in the middle of your second line is "dangerous", since the expression immediately to the left of it will not necessarily be equal to the one immediately to the right when solving DEs. (Here, it could be correct, if the negative wasn't dropped.) It's best to write a new line. The last part of the second line has a problem. Where did the negative go?
stephenB 27 Jan 2018, 02:03
Integrating both sides of
`int 1/(-3x) dx = int 1/y dy`
gives
`-1/3 ln|x| = ln|y| + K` (including the `-` sign that was missing from the OP's answer)
The question says `y(1)= e,` so to find the value of `K` we substitute:
`-1/3 ln|1| = ln|e| + K`
`ln|1| = 0` and `ln|e| = 1`, so we have
`0 = 1 + K`, so
`K=-1`
So the answer is
`-1/3 ln|x| = ln|y| - 1`
We can express it in terms of `y` fairly easily:
Add `1` to both sides:
`-1/3 ln|x| + 1 = ln|y|`
Since `log(a^b) = b log a`, we can write:
`ln|x^(-1/3)| + 1 = ln|y|`
and `ln(e) = 1`, so we can put:
`ln|x^(-1/3)| + ln(e) = ln|y|`
Using `log(ab) = log(a) + log(b)`, we can combine the LHS:
`ln|ex^(-1/3)| = ln|y|`
Taking "`e` to both sides" (i.e., finding the antilogarithms), we have:
`y = ex^(-1/3)`
X
Integrating both sides of `int 1/(-3x) dx = int 1/y dy` gives `-1/3 ln|x| = ln|y| + K` (including the `-` sign that was missing from the OP's answer) The question says `y(1)= e,` so to find the value of `K` we substitute: `-1/3 ln|1| = ln|e| + K` `ln|1| = 0` and `ln|e| = 1`, so we have `0 = 1 + K`, so `K=-1` So the answer is `-1/3 ln|x| = ln|y| - 1` We can express it in terms of `y` fairly easily: Add `1` to both sides: `-1/3 ln|x| + 1 = ln|y|` Since `log(a^b) = b log a`, we can write: `ln|x^(-1/3)| + 1 = ln|y|` and `ln(e) = 1`, so we can put: `ln|x^(-1/3)| + ln(e) = ln|y|` Using `log(ab) = log(a) + log(b)`, we can combine the LHS: `ln|ex^(-1/3)| = ln|y|` Taking "`e` to both sides" (i.e., finding the antilogarithms), we have: `y = ex^(-1/3)`
Murray 27 Jan 2018, 02:14
As usual, a good quality answer, stephenB.
X
As usual, a good quality answer, stephenB.