8. Damping and the Natural Response in RLC Circuits
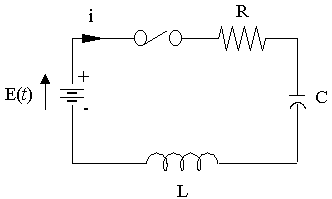
Consider a series RLC circuit (one that has a resistor, an inductor and a capacitor) with a constant driving electro-motive force (emf) E. The current equation for the circuit is
`L(di)/(dt)+Ri+1/Cinti\ dt=E`
This is equivalent: `L(di)/(dt)+Ri+1/Cq=E`
Differentiating, we have
`L(d^2i)/(dt^2)+R(di)/(dt)+1/Ci=0`
This is a second order linear homogeneous equation.
Its corresponding auxiliary equation is
`Lm^2+Rm+1/C=0`
with roots:
`m_1=(-R)/(2L)+(sqrt((R^2-4L"/"C)))/(2L)`
`=-alpha+sqrt(alpha^2-omega_0^2`
`m_2=(-R)/(2L)-(sqrt((R^2-4L"/"C)))/(2L)`
`=-alpha-sqrt(alpha^2-omega_0^2`
Now
`alpha=R/(2L)` is called the damping coefficient of the circuit
`omega_0 = sqrt(1/(LC)`is the resonant frequency of the circuit.
m1 and m2 are called the natural frequencies of the circuit.
The nature of the current will depend on the relationship between R, L and C.
There are three possibilities:
Case 1: R2 > 4L/C (Over-Damped)
Graph of overdamped case.
Here both m1 and m2 are real, distinct and negative. The general solution is given by
`i(t)=Ae^(m_1t)+Be^(m_2t)`
The motion (current) is not oscillatory, and the vibration returns to equilibrium.
Case 2: R2 = 4L/C (Critically Damped)
Graph of critcally damped case.
Here the roots are negative, real and equal,
i.e. `m_1= m_2= -R/(2L)`.
The general solution is given by
`i(t)=(A+Bt)e^(-Rt"/"2L)`
The vibration (current) returns to equilibrium in the minimum time and there is just enough damping to prevent oscillation.
Case 3: R2 < 4L/C (Under-Damped)
Graph of RLC under-damped case.
Here the roots are complex where
`m_1=alpha+jomega`, and `m_2=alpha-jomega`
The general solution is given by
`i(t)=e^(-alpha t)(A\ cos\ omegat+B\ sin\ omegat)`
where
`\alpha = R/(2L)` is called the damping coefficient, and `omega` is given by:
`omega=sqrt(1/(LC)-R^2/(4L^2)`
In this case, the motion (current) is oscillatory and the amplitude decreases exponentially, bounded by
`i=+-sqrt(A^2+B^2)\ e^(-Rt"/"2L)`
as we can see in the diagram above.
When R = 0, the circuit displays its natural or resonant frequency, `omega_0=sqrt(1/(LC))`.
Example
In a series RCL circuit driven by a constant emf, the natural response of the circuit is given by
`(d^2i)/(dt^2)+4(di)/(dt)+4i=0`
for which the initial conditions are i(0) = 2 A and `(di)/(dt)` at t = 0 is 4.
State the nature of response of the current and hence solve for i.
Answer
Two ways of solving this problem are shown here. You can choose whichever one makes more sense to you, or seems easiest.
Solution: Alternative 1
We will solve this in the same way as the previous section, 2nd Order Linear DEs.
A.E. `m^2+4m+4`
Solutions are a repeated root: `m_1=-2`, and `m_2=-2`
The response is critically damped, since the roots are equal.
`i(t)=(A+Bt)e^(-2t)`
`i(0)=2` implies `A=2`
So we can now write:
`i(t)=(2+Bt)e^(-2t)`
Differentiating gives:
`(di)/(dt)=(2+Bt)(-2e^(-2t))+Be^(-2t)`
`[(di)/(dt)]_(t=0)=4 `
This implies:
`(2)(-2)+B(1)=4 `
So `B=8`
Therefore `i(t)=(2+8t)e^(-2t)`
Solution: Alternative 2
Using the variables given in the damping theory above:
`L=1`, `R=4`, `1/C=4`, so `C=1/4`
`R^2=16`
`(4L)/C=4/(1"/"4)=16`
So `R^2=(4L)/C` and therefore we have critical damping.
Now `m_1=m_2=-R/(2L)=-4/2=-2`
The general solution is given by `i(t)=(A+Bt)e^(-Rt"/"2L`
So `i(t)=(A+Bt)e^(-4t"/"(2xx1))` `=(A+Bt)e^(-2t)`
This is the same solution we have using Alternative 1. The rest of the solution (finding A and B) will be identical.
Solution using Scientific Notebook
We need to set up the 2nd order DE with initial conditions as follows.
`(d^2i)/(dt^2)+4(di)/(dt)+4i=0`
`i(0)=2`
`i^'(0)=4`
[Then go to Compute menu, Solve ODE..., Exact]
The graph of our solution is:
Graph of `i(t)=(2+8t)e^(-2t)`, a critcally damped case.