Hasham 19 Dec 2015, 03:01
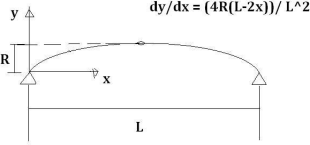
What is the length of the parabola where dy/dx = (4Rx(L-2x)) / L^2? Here's the diagram:
5. Integration: Other Trigonometric Forms
I tried to use the arc length formula but there were too many letters in the problem.
X
What is the length of the parabola where dy/dx = (4Rx(L-2x)) / L^2? Here's the diagram: <img src="/forum/uploads/parabola310.png" width="310" height"145" alt="parabola" />
Relevant page <a href="/methods-integration/5-integration-other-trigonometric-forms.php">5. Integration: Other Trigonometric Forms</a> What I've done so far I tried to use the arc length formula but there were too many letters in the problem.
Murray 19 Dec 2015, 20:39
Hi again
You are encouraged to use the math entry system so it's easier for you (and us) to read your math.
At least show us your first steps so we can guide you better.
Gentle warning: This has a really complicated solution. We'll get started and I'll stop you before it's too late.
X
Hi again You are encouraged to use the math entry system so it's easier for you (and us) to read your math. At least show us your first steps so we can guide you better. <b>Gentle warning:</b> This has a really complicated solution. We'll get started and I'll stop you before it's too late.
Hasham 20 Dec 2015, 08:32
I get it a bit more now. They are already giving me the `dy/dx` in the question. Here's what I've got:
`s=inta^b sqrt(1+(dy/dx)^2)`
`s=inta^b sqrt(1+((4R(L-2x))/L^2)^2)`
`s=inta^b sqrt(1+((16R^2(L^2-4Lx+4x^2))/L^4))`
I'm stuck there
X
I get it a bit more now. They are already giving me the `dy/dx` in the question. Here's what I've got: `s=inta^b sqrt(1+(dy/dx)^2)` `s=inta^b sqrt(1+((4R(L-2x))/L^2)^2)` `s=inta^b sqrt(1+((16R^2(L^2-4Lx+4x^2))/L^4))` I'm stuck there
Murray 21 Dec 2015, 11:13
Get everything under the square root, over `L^4`
X
Get everything under the square root, over `L^4`
Hasham 22 Dec 2015, 00:03
OK.
`s=inta^b sqrt( (L^4+16R^2(L^2-4Lx+4x^2))/L^4)`
`=1/(L^2) inta^b sqrt( L^4+16R^2(L^2-4Lx+4x^2))`
`=1/(L^2) inta^b sqrt( L^4+16R^2 L^2-64R^2Lx+ 64R^2 x^2)`
I'm stuck again. And what's `a` and `b`?
X
OK. `s=inta^b sqrt( (L^4+16R^2(L^2-4Lx+4x^2))/L^4)` `=1/(L^2) inta^b sqrt( L^4+16R^2(L^2-4Lx+4x^2))` `=1/(L^2) inta^b sqrt( L^4+16R^2 L^2-64R^2Lx+ 64R^2 x^2)` I'm stuck again. And what's `a` and `b`?
Murray 23 Dec 2015, 02:43
Yes, that's good. But that's really the limit of reasonable calculation. The integral from there is really ugly.
For `a` and `b`, go back to your diagram.
Where is the origin? What are the `x`-coordinates of the far left and far right points of the parabola?
X
Yes, that's good. But that's really the limit of reasonable calculation. The integral from there is really ugly. For `a` and `b`, go back to your diagram. Where is the origin? What are the `x`-coordinates of the far left and far right points of the parabola?
Hasham 23 Dec 2015, 22:38
`a=0` and `b=L`, correct?
So the integral will be
`s=1/(L^2) int0^L sqrt( L^4+16R^2 L^2-64R^2Lx+ 64R^2 x^2)`
If we have values for `R` and `L`, can it be done?
X
`a=0` and `b=L`, correct? So the integral will be `s=1/(L^2) int0^L sqrt( L^4+16R^2 L^2-64R^2Lx+ 64R^2 x^2)` If we have values for `R` and `L`, can it be done?
Murray 24 Dec 2015, 19:09
I put it into Wolfram|Alpha with values `L=10` and `R=3`. The answer was `12.04`.
You can see the numeric solution here:
Numeric solution with L=10 and R=3
and the (horrible) algebraic answer here:
integral 1/L^2 (sqrt( L^4+16*R^2*L^2-64*R^2*L*x+ 64*R^2*x^2))dx - Wolfram|Alpha
Definitely not something we should be doing on paper!
X
I put it into Wolfram|Alpha with values `L=10` and `R=3`. The answer was `12.04`. You can see the numeric solution here: <a href="http://www.wolframalpha.com/input/?i=integral+from+0+to+10+0.01*%28sqrt%28+L^4%2B16*R^2*L^2-64*R^2*L*x%2B+64*R^2*x^2%29%29dx+where+L+%3D+10+and+R+%3D+3">Numeric solution with L=10 and R=3</a> and the (horrible) algebraic answer here: <a href="http://www.wolframalpha.com/input/?i=integral+1%2FL^2+%28sqrt%28+L^4%2B16*R^2*L^2-64*R^2*L*x%2B+64*R^2*x^2%29%29dx"> integral 1/L^2 (sqrt( L^4+16*R^2*L^2-64*R^2*L*x+ 64*R^2*x^2))dx - Wolfram|Alpha</a> Definitely not something we should be doing on paper!
X
I agree! Thanks a lot.
You need to be logged in to reply.