Head Injury Criterion (HIC) pt 2: HIC Index, example

Experiments showed researchers that the Severity Index did not accurately describe the likelihood of certain injuries in a crash.

They subsequently developed the Head Injury Criterion (HIC), which is based on the average value of the acceleration over the most critical part of the deceleration (shown in the blue rectangles in the Mercedes data before).

We met average value of a function earlier in this chapter.

The average value `bar(a)` of the acceleration a(t) over the time interval t₁ to t₂ is given by

`bar a=1/(t_2-t_1)int_(t_1)^(t_2)a(t)\ dt`

For the HIC, this was modified (based on experimental data) as follows:

`HIC=` `{:"max" (t_1\ "or"\ t_2):}` `{(t_2-t_1)[1/(t_2-t_1)int_(t_1)^(t_2)a(t)dt]^2.5}`

The formula means:

The HIC is the maximum value over the critical time period t₁ to t₂ for the expression in braces, { }. The index 2.5 is chosen for the head, based on experiments.

Modelling a crash test result

Let's see an example of the HIC in use. We'll model one of the Mercedes Benz crash results and then apply our formula.

Developing the model

Our approach is to model the deceleration curve with a function. We recognise that the shape of the crash data graph is basically like the curve:

`f(x)=1/(x^2+1)`

(This similar to the 'bell-shaped curve' in statistics.)

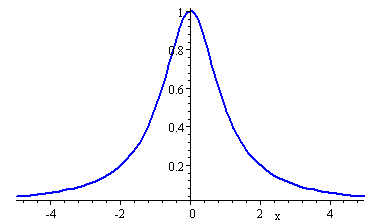
Model for the Acceleration

By modifying the function above, we can get curves very close to the Mercedes experimental data.

`a(t)=` `16400/((t-68)^2+400)` `+1480/((t-93)^2+18)`

This model was obtained by observing 2 peaks in the deceleration graph, centred at 68 ms and 93 ms. By adding the 2 bell-like curves, we get a model very close to the required graph:

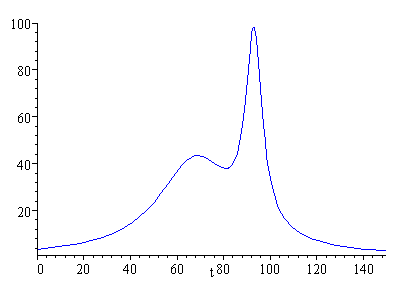
The computer time to calculate the HIC expression is high, so we need to simplify things a bit.

We can simplify that part of the HIC formula in braces, { }, for different values of d = t₂ − t₁. We define a family of curves:

`H_(t,d)=d(1/dint_t^(t+d)a(T)dT)^2.5`

We then vary the value of d. The value of the highest peak of the family of curves obtained gives us the HIC.

HIC without Airbag

We now use the model for a(t) from above and maximise the value of H for different values of d.

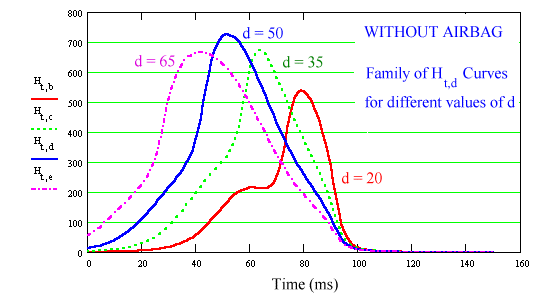
We see that the highest peak occurs when `d=50` and reading from the graph we see that the HIC is approximately `725`. This is reasonably close to the Mercedes Benz data. (Other values for d are shown, but not all, of course. The value d = 50 did in fact give the highest curve.)

HIC with Airbag

The model is simpler for the airbag case, as the deceleration is smoother and is almost bell-shaped. Some modelling achieves the following expression for the acceleration:

`a(t)=22000/((t-74)^2+500)`

The graph is as follows (drawn with the same vertical scale as the non-airbag case):

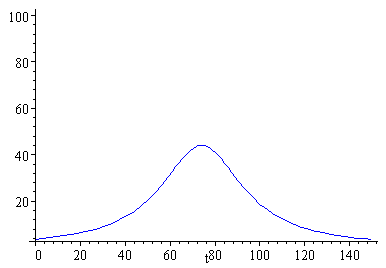
Now to apply the formula for H again. We get a family of curves and once again, `d = 50` gives us the maximum value, hence the HIC.

The HIC for the airbag case is around `310`, close to the Mercedes Benz data.

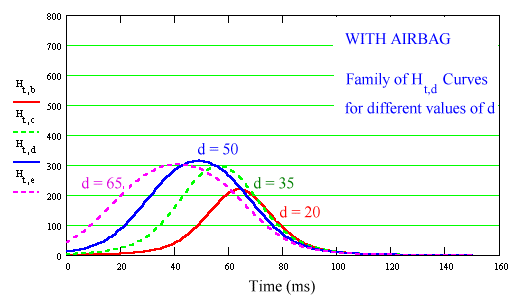
Our main aim here is to reduce the effects of rapid deceleration. If the curve is low and flat, injury to the head is reduced.

The Head Injury Criterion (HIC) - What Does it all Mean?

Generally, experts agree that HIC values above 1000 are life threatening.

Some crash tests have HIC values as low as 142 (an Audi 8, with airbag, in 1995).

Conclusions

• You cannot hold a child firmly in your arms in a crash
• Safety belts save lives
• Airbags save heads
• Areas under curves and average values have interesting applications.

Reference: Henn, H Crash Tests and the Head Injury Criterion, Teaching Mathematics and its Applications, Vol 17, No 4, 1998.