1. Derivatives of the Sine, Cosine and Tangent Functions
by M. Bourne
It can be shown from first principles that:
`(d(sin x))/(dx)=cos x`
`(d(cos x))/dx=-sin x`
`(d(tan x))/(dx)=sec^2x`
Explore animations of these functions with their derivatives here:
Differentiation Interactive Applet - trigonometric functions.
In words, we would say:
The derivative of sin x is cos x,
The derivative of cos x is −sin x (note the negative sign!) and
The derivative of tan x is sec2x.
Now, if u = f(x) is a function of x, then by using the chain rule, we have:
`(d(sin u))/(dx)=cos u(du)/(dx)`
`(d(cos u))/dx=-sin u(du)/(dx)`
`(d(tan u))/(dx)=sec^2u(du)/(dx)`
Example 1
Differentiate `y = sin(x^2 + 3)`.
Answer
First, let: `u = x^2+ 3` and so `y = sin u`.
We have:
IMPORTANT:`(dy)/(dx)=(dy)/(du)(du)/(dx)`
`=cos u(du)/(dx)`
`=cos(x^2+3)(d(x^2+3))/(dx)`
`=2x\ cos(x^2+3)`
cos x2 + 3
does not equal
cos(x2 + 3).
The brackets make a big difference. Many students have trouble with this.
Here are the graphs of y = cos x2 + 3 (in green) and y = cos(x2 + 3) (shown in blue).
The first one, y = cos x2 + 3, or y = (cos x2) + 3, means take the curve y = cos x2 and move it up by `3` units.
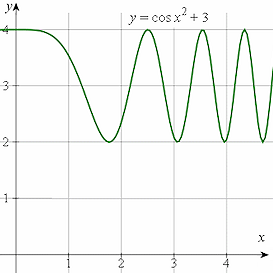
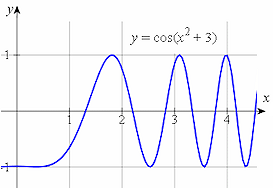
The second one, y = cos(x2 + 3), means find the value (x2 + 3) first, then find the cosine of the result.
They are quite different!
Example 2
Find the derivative of `y = cos 3x^4`.
Answer
Let u = 3x4 and so `y = cos u`.
Then
`(dy)/(dx)=(dy)/(du)(du)/(dx)`
`=-sin u(du)/(dx)`
`=-sin(3x^4)(d(3x^4))/(dx)`
`=-12x^3sin 3x^4`
Example 3
Differentiate `y = cos^3 2x`
Answer
This example has a function of a function of a function.
Let `u = 2x` and `v = cos 2x`
So we can write `y = v^3` and `v = cos\ u`
`(dy)/(dx)=(dy)/(dv)(dv)/(du)(du)/(dx)`
`=3v^2(-sin u)(2)`
`=3(cos^2 2x)(-sin 2x)(2)`
`=-6\ cos^2 2x\ sin 2x`
Example 4
Find the derivative of `y = 3 sin 4x + 5 cos 2x^3`.
Answer
In the final term, put u = 2x3.
We have: `y=3 sin 4x+5 cos 2x^3` `(dy)/(dx)=(3)(cos 4x)(4)+` `(5)(-sin 2x^3)(6x^2)` `=12 cos 4x-30x^2 sin 2x^3`
Exercises
1. Differentiate y = 4 cos (6x2 + 5).
Answer
Put u = 6x2 + 5, so y = 4 cos u.
So
`(dy)/(dx)=(dy)/(du)(du)/(dx)`
`=4[-sin(6x^2+5)][(12x)]`
`=-48x\ sin(6x^2+5)`
2. Find the derivative of y = 3 sin3 (2x4 + 1).
Answer
Put u = 2x4 + 1 and v = sin u
So y = 3v3
`(dy)/(dx)=(dy)/(dv)(dv)/(du)(du)/(dx)`
`=[9v^2][cos u][8x^3]`
`=[9\ sin^2u][cos(2x^4+1)][8x^3]`
`=72x^3sin^2(2x^4+1)cos(2x^4+1)`
3. Differentiate y = (x − cos2x)4.
Answer
Put u = x − cos2x and then y = u4.
Now
`(du)/(dx)=1-2\ cos x(-sin x)`
`=1+2\ sin x\ cos x`
and
`(dy)/(du)=4u^3`
So we have:
`(dy)/(dx)=(dy)/(du)(du)/(dx)`
`=4u^3(du)/(dx)`
`=4[x-cos^2x]^3[1+` `{:2 sin x cos x]`
4. Find the derivative of:
`y=(2x+3)/(sin 4x)`
Answer
Put u = 2x + 3 and v = sin 4x
Now
`(dv)/(dx)=4\ cos 4x`
So using the quotient rule, we have:
`(dy)/(dx) =(v(du)/(dx)-u(dv)/(dx))/v^2`
`=((sin 4x)(2)-(2x+3)(4\ cos 4x))/(sin^2 4x)`
`=(2\ sin 4x-4(2x+3)cos 4x)/(sin^2 4x)`
5. Differentiate y = 2x sin x + 2 cos x − x2cos x.
Answer
First, we write the right hand side as:
`y = 2x\ sin x + (2 − x^2) cos x`.
We have 2 products. The first term is the product of `(2x)` and `(sin x)`. The second term is the product of `(2-x^2)` and `(cos x)`.
So, using the Product Rule on both terms gives us:
`(dy)/(dx)= (2x) (cos x) + (sin x)(2) +` ` [(2 − x^2) (−sin x) + (cos x)(−2x)]`
`= cos x (2x − 2x) + ` `(sin x)(2 − 2 + x^2)`
`= x^2sin x`
6. Find the derivative of the implicit function
x cos 2y + sin x cos y = 1.
Answer
The implicit function:
`x\ cos 2y+sin x\ cos y=1`
We differentiate each term from left to right:
`x(-2\ sin 2y)((dy)/(dx))` `+(cos 2y)(1)` `+sin x(-sin y(dy)/(dx))` `+cos y\ cos x`
`=0`
So
`(-2x\ sin 2y-sin x\ sin y)((dy)/(dx))` `=-cos 2y-cos y\ cos x`
Solving for `dy/dx` gives us:
`(dy)/(dx)=(-cos 2y-cos y\ cos x)/(-2x\ sin 2y-sin x\ sin y)`
`= (cos 2y+cos x\ cos y)/(2x\ sin 2y+sin x\ sin y)`
7. Find the slope of the line tangent to the curve of
`y=(2 sin 3x)/x`
where `x = 0.15`
Answer
`(dy)/(dx)=(x(6\ cos 3x)-(2\ sin 3x)(1))/x^2`
`=(6x\ cos 3x-2\ sin 3x)/x^2`
When `x = 0.15` (in radians, of course), this expression (which gives us the slope) equals `-2.65`.
Here is a graph of our situation. The tangent to the curve at the point where `x=0.15` is shown. Its slope is `-2.65`.
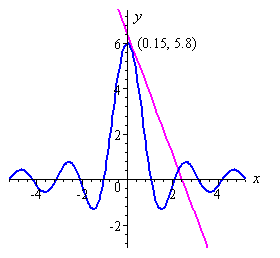
8. The current (in amperes) in an amplifier circuit, as a function of the time t (in seconds) is given by
`i = 0.10 cos (120πt + π/6)`.
Find the expression for the voltage across a 2.0 mH inductor in the circuit, given that
`V_L=L(di)/(dt)`
Answer
` V_L =L(di)/(dt)`
`=0.002(di)/(dt)`
`=0.002(0.10)(120pi)` `xx(-sin(120pit+pi/6))`
`=-0.024pi\ sin(120pit+pi/6)`
9. Show that y = cos3x tan x satisfies
`cos x(dy)/(dx)+3y sin x-cos^2x=0`
Answer
The right hand side is a product of (cos x)3 and (tan x).
Now (cos x)3 is a power of a function and so we use Differentiating Powers of a Function:
`d/(dx)u^3=3u^2(du)/(dx)`
With u = cos x, we have:
`d/(dx)(cos x)^3=3(cos x)^2(-sin x)`
Now, from our rules above, we have:
`d/(dx)tan x=sec^2x`
Using the Product Rule and Properties of tan x, we have:
`(dy)/(dx)`
`=[cos^3x\ sec^2x]` `+tan x[3(cos x)^2(-sin x)]`
`=(cos^3x)/(cos^2x)` `+(sin x)/(cos x)[3(cos x)^2(-sin x)]`
`=cos x-3\ sin^2x\ cos x`
We need to determine if this expression creates a true statement when we substitute it into the LHS of the equation given in the question.
` "LHS"`
`=cos x(dy)/(dx)` `+3y\ sin x-cos^2x`
`=cos x(cos x-3\ sin^2x\ cos x)` `+3(cos^3x\ tan x)sin x-cos^2x`
`=cos^2x` `-3\ sin^2x\ cos^2x` `+3\ sin^2x\ cos^2x` `-cos^2x`
`=0`
` ="RHS"`
We have shown that it is true.
10. Find the derivative of y = x tan x
Answer
This is the product of `x` and `tan x`.
So we have:
`d/(dx)(x\ tan x) =(x)(sec^2x)+(tan x)(1)`
`=x\ sec^2x+tan x`
Problem Solver
Need help solving a different Trigonometry problem? Try the Problem Solver.
Disclaimer: IntMath.com does not guarantee the accuracy of results. Problem Solver provided by Mathway.
See also: Derivative of square root of sine x by first principles.