6. Application: Series RC Circuit
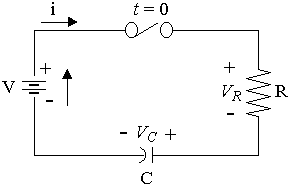
An RC series circuit
In this section we see how to solve the differential equation arising from a circuit consisting of a resistor and a capacitor. (See the related section Series RL Circuit in the previous section.)
In an RC circuit, the capacitor stores energy between a pair of plates. When voltage is applied to the capacitor, the charge builds up in the capacitor and the current drops off to zero.
Case 1: Constant Voltage
The voltage across the resistor and capacitor are as follows:
`V_R= Ri`
and
`V_C=1/Cinti dt`
Kirchhoff's voltage law says the total voltages must be zero. So applying this law to a series RC circuit results in the equation:
`Ri+1/Cinti dt=V`
One way to solve this equation is to turn it into a differential equation, by differentiating throughout with respect to t:
`R(di)/(dt)+i/C=0`
Solving the equation gives us:
`i={V}/Re^(-t"/"RC)`
Proof
We start with:
`R(di)/(dt)+i/C=0`
Divide through by R:
`(di)/(dt)+(1/(RC))i=0`
We recognise this as a first order linear differential equation.
Identify P and Q:
`P=1/(RC)`
Q = 0
Find the integrating factor (our independent variable is t and the dependent variable is i):
`intP dt=int1/(RC)dt` `=1/(RC)t`
So
`IF=e^(t"/"RC`
Now for the right hand integral of the 1st order linear solution:
`intQe^(intPdt)dt=int0 dt=K`
Applying the linear first order formula:
`ie^(t"/"RC)=K`
Since `i = V/R` when `t = 0`:
`K=V/R`
Substituting this back in:
`ie^(t"/"RC)=V/R`
Solving for i gives us the required expression:
`i=V/Re^(-t"/"RC)`
Important note: We are assuming that the circuit has a constant voltage source, V. This equation does not apply if the voltage source is variable.
The time constant in the case of an RC circuit is:
τ = RC
The function
`i=V/Re^(-t"/"RC)`
has an exponential decay shape as shown in the graph. The current stops flowing as the capacitor becomes fully charged.
Graph of `i=V/R e^(-(t"/"RC))`, an exponential decay curve.
Applying our expressions from above, we have the following expressions for the voltage across the resistor and the capacitor:
`V_R=Ri=Ve^(-t"/"RC)`
`V_C=1/Cinti dt=V(1-e^(-t"/"RC))`
While the voltage over the resistor drops, the voltage over the capacitor rises as it is charged:
Graphs of `V_R=Ve^(-t"/"RC)` (in green) and `V_C=V(1-e^(-t"/"RC))` (in gray).
Case 2: Variable Voltage and 2-mesh Circuits
We need to solve variable voltage cases in q, rather than in i, since we have an integral to deal with if we use i.
So we will make the substitutions:
`i=(dq)/(dt)`
and
`q=int i dt`
and so the equation in i involving an integral:
`Ri+1/Cinti dt=V`
becomes the differential equation in q:
`R(dq)/(dt)+1/Cq=V`
Example 1
A series RC circuit with R = 5 W and C = 0.02 F is connected with a battery of E = 100 V. At t = 0, the voltage across the capacitor is zero.
(a) Obtain the subsequent voltage across the capacitor.
(b) As t → ∞, find the charge in the capacitor.
Answer
We will solve this 3 ways, since it has a constant voltage source:
1 and 2: Solving the DE in q, as:
- a linear DE and
- variables separable
3. Using the formulas `V_C=V(1-e^(-t"/"RC))` and `i=V/R e^(-t"/"RC`.
Method 1 - Solving the DE in q
From the formula: `Ri + 1/C int i dt=V`, we obtain:
`R(dq)/(dt)+1/Cq=V`
On substituting, we have:
`5(dq)/(dt)+1/0.02q=100`
`5(dq)/(dt)+50q=100`
`(dq)/(dt)+10q=20`
We can solve this DE 2 ways, since it is variables separable or we could do it as a linear DE. The algebra is easier if we do it as a linear DE.
Solving this differential equation as a linear DE, we have:
`"IF"=e^(10t`
So `qe^(10t)=int (e^(10t))20 dt` `=2e^(10t)+K`
So `q=2+Ke^(-10t)`
Now, since `q(0)=0`, (that is, when `t=0`, `q=0`) this gives: `K=-2`.
So `q=2(1-e^(-10t))`.
Graph of `q=2(1-e^(-10t))`, solution of a differential equation.
As `t->oo`, `q->2\ "C"`.
Now,
`V_C=1/Cinti dt`
`=1/Cq`
`=1/0.02 2(1-e^(-10t))`
`=100(1-e^(10t)) `
For comparison, here is the solution of the DE using variables separable:
`(dq)/(dt)=10(2-q)`
`(dq)/(2-q)=10dt`
` -ln |2-q|=10t+K`
(We could continue and get the same expression as above.)
Since `t=0`, `q=0`, we have `K=-ln 2`.
So
`-ln |2-q|=10t-ln 2`
` -ln 2+ln |2-q|=-10t`
`(2-q)/2=e^(-10t)`
` 2-q=2e^(-10t)`
` q=2(1-e^(-10t))`
Method 2:
We use the formulae `V_C=V(1-e^(-t"/"RC))` and `i=V/R e^(-t"/"RC)`.
Now `1/(RC)=1/(5xx0.02)=10`
So:
`V_C=V(1-e^(-t"/"RC))` `=100(1-e^(-10t))`
`i=V/Re^(-t"/"RC)`
`=100/5e^(-t"/"0.1) `
`=20e^(-10t) `
Now
`q=inti dt`
`=int20e^(-10t)dt`
`=-2e^(-10t)+K_1`
From here, we use `q(0)=0` and obtain: `K_1=2.`
So `q=2(1-e^(-10t))`, as before. Also, as `t->oo`, `q->2\ "C"`.
Example 2
Find the charge and the current for t > 0 in a series RC circuit where R = 10 W, C = 4 × 10-3 F and E = 85 cos 150t V.
Assume that when the switch is closed at t = 0, the charge on the capacitor is -0.05 C.
Answer
We will solve this 2 ways:
1. Solving in q.
2. Using Scientific Notebook.
[NOTE: We cannot use the formulae `V_C=V(1-e^(-t"/"RC))` and `i=V/re^(-t"/"RC)`, since the voltage source is not constant.]
From the formula: `Ri+1/Cint i dt=V`, we obtain:
`R(dq)/(dt)+1/Cq=V`
Since `R=10`, `C=4xx10^-3`, and `V=85 cos 150t`, we have:
`10(dq)/(dt)+1/(4xx10^-3)q=85 cos 150t`
`10(dq)/(dt)+250q=85 cos 150t`
`(dq)/(dt)+25q=8.5 cos 150t`
Now, we can solve this differential equation in q using the linear DE process as follows:
`"IF"=e^(25t)`
`e^(25t)q=inte^(25t)8.5 cos 150t dt` `=8.5inte^(25t)cos 150t dt`
Then we use the integration formula (found in our standard integral table):
`inte^(mt)cos nt dt=` `(e^(mt))/(m^2+n^2)(m cos nt+n sin nt)`
We obtain:
`e^(25t)q=8.5inte^(25t) cos 150t dt`
`=8.5(e^(25t))/23125(25 cos 150t+` `{:150e^(25t) sin 150t)`
`=0.0092e^(25t) cos 150t+` `0.055e^(25t) sin 150t+K`
Dividing throughout by `e^(25t` gives:
`q=0.0092 cos 150t+` `0.055 sin 150t+` `Ke^(-25t)`
We now need to find `K`:
`q(0)=-0.05` means `K=-0.05-0.0092` `=-0.0592`
So this gives us:
`q=0.0092 cos 150t+` `0.055 sin 150t-` `0.0592e^(-25t)`
Method Using Scientific Notebook
We set up the differential equation and the initial conditions in a matrix (not a table) as follows:
`(dq)/(dt)+25q=8.5 cos 150t`
`q(0)=-0.05`
Choosing Solve ODE - Exact from the Compute menu gives:
Exact solution is:
`q(t)=0.0092 cos 150t+` `0.055 sin 150t-` `0.059e^(-25t)`
The graph for `q(t)` is as follows:
Graph of current `q` at time `t`. It's in steady state by around `t=0.12`.
We are also asked to find the current. We simply differentiate the expression for q:
`i` `=d/(dt)(0.0092 cos 150t+` `{:0.055 sin 150t-0.0592e^(-25t))` `=-1.38 sin 150t+` `8.25 cos 150t+` `1.48e^(-25t)`
The graph for i(t):
Graph of current `i` at time `t`. It's also in steady state by around `t=0.12`.
Example 3
In the RC circuit shown below, the switch is closed on position 1 at t = 0 and after 1 τ is moved to position 2. Find the complete current transient.
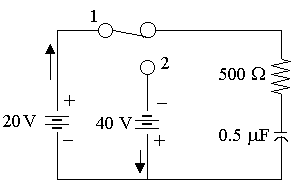
Answer
At t = 0, the switch is at Position 1.
We note that `q(0)=0`.
`R(dq_1)/(dt)+1/Cq_1=V`
`500(dq_1)/(dt)+1/(0.5xx10^-6)q_1=20`
`(dq_1)/(dt)+4000q_1=0.04`
Using SNB to solve this differential equation, we have:
`q_1(t)=1/(100,000)(1-e^(-4,000t))`
NOTE: By differentiating, this gives us:
`i_1(t)=` `d/(dt)1/100000(1-e^(-4000t))=` `0.04e^(-4000t`
We need to find `tau`:
`tau=RC=500xx0.5xx10^-6=` `0.00025`.
Now, at `t=0.00025`, the charge will be:
`q_1(0.00025)`
`=[1/(100,000)(1-e^(-4,000t))]_(t=0.00025)`
`=6.3212xx10^-6`
Position 2
At `t=tau`, switch at Position 2:
Applying the formula `R(dq_2)/(dt)+1/Cq_2=V` again:
`500(dq_2)/(dt)+1/(0.5xx10^-6)q_2=-40`
NOTE: The negative voltage is because the current will flow in the opposite direction through the resistor and capacitor.
Once again, we solve using Scientific Notebook:
`500(dq_2)/(dt)+1/(0.5xx10^-6)q_2=-40`
` q_2(0)=6.3212xx10^-6`
Exact solution is:
`q_2(t)` `=-0.00002+2.6321xx10^-5e^(-4000t)`
So the current transient will be:
`i_2=(dq_2)/(dt)`
`=d/(dt)(-0.00002+2.6321xx10^-` `{:5e^(-4000t))`
`=-0.10528e^(-4000t)`
This expression assumes that time starts at `t=0`. However, we moved the switch to Position 2 at `t=0.00025`, so we need:
`i_2=-0.10528e^(-4000(t-0.00025))` `=-0.10528e^(1-4000t`
So the complete current transient is:
`i_1(t)=0.04e^(-4000t)` for `0 <= t <= 0.00025`
`i_2(t)=-0.10528e^(1-4000t)` for `t>0.00025`
The graph is quite interesting:
Graph of current `i` at time `t`.
Do not try this next one at home!
Here's a great Java-based RLC simulator (on an external site). He is actually making a coil gun. You can play with each of V, R, L and C and see the effects. Play and learn :-)
Sorry, it won't work on a mobile device.