2. Separation of Variables
Later, on this page...
Some differential equations can be solved by the method of separation of variables (or "variables separable") . This method is only possible if we can write the differential equation in the form
A(x) dx + B(y) dy = 0,
where A(x) is a function of x only and B(y) is a function of y only.
Once we can write it in the above form, all we do is integrate throughout, to obtain our general solution.
NOTE: In this variables separable section we only deal with first order, first degree differential equations.
Example 1 - Separation of Variables form
a) The differential equation (which we saw earlier in Solutions of Differential Equations):
`(dy)/(dx)ln\ x-y/x=0`
can be expressed in the required form, A(x) dx + B(y) dy = 0, after some algebraic juggling:
` (dy)/(dx)ln\ x-y/x=0`
`dy\ ln\ x-(y\ dx)/x=0`
`dy-(y\ dx)/(x\ ln\ x)=0`
`(dy)/y-(dx)/(x\ ln\ x)=0`
`1/ydy-1/(x\ ln\ x)dx=0`
Here, `A(x) = -1/(x\ ln\ x)` and `B(y) = 1/y`.
[To solve the equation, we would then integrate throughout].
b) The following differential equation cannot be expressed in the required form, so it cannot be solved using separation of variables:
`(dy)/(dx)=(3(x+y))/(x(y-2))`
Example 2
Solve the differential equation:
y2 dy + x3 dx = 0
Answer
This is already in the required form (since the x-terms are together with dx terms, and y-terms are together with dy terms), so we simply integrate:
`inty^2dy+intx^3dx=0`
Giving:
`y^3/3+x^4/4=K`
This is the general solution for the differential equation.
We can continue on to solve this as an explicit function in x, as follows:
`y^3=3(K-x^4/4)`
`y=root(3)(3(K-x^4/4))`
Taking a typical constant value `K=5`, we have this solution graph:
Typical solution graph `y=root(3)(3(5-x^4/4))`.
Example 3
Solve the differential equation: `2(dy)/(dx)=(y(x+1))/x`
Answer
First we must separate the variables:
`(2\ dy)/y=((x+1)dx)/x`
This gives us: `(2\ dy)/y=(1+1/x)dx`
We now integrate:
`int(2 dy)/y=int(1+1/x)dx`
`2 ln y=x+ln x+K`
Go back to Integration: Basic Logarithm Form if you are rusty on this integration.
We could continue with our solution and express `y` as an explicit function of `x`, as follows:
`ln y=(x+ln x+K)/2`
`y=e^((x+ln x+K)//2)`
Taking a typical constant value `K=1`, we have this solution graph:
Typical solution graph `y=e^((x+ln x+1)//2)`.
Example 4
Solve `t(dx)/(dt)-x=3`
Answer
`t(dx)/(dt)-x=3`
We want all x's on one side, all the terms in t on the other.
`t(dx)/(dt)=x+3`
Divide both sides by `(x + 3)` and multiply both sides by `dt`:
`t(dx)/(x+3)=dt`
Next, divide both sides by t.
`(dx)/(x+3)=(dt)/t`
Integrate both sides.
`int(dx)/(x+3)=int(dt)/t`
Important: dx and dt must be on top of the fraction (i.e. in the numerator).
`ln|x+3|=ln|t|+C`
Take "e to power of both sides":
`x+3=e^(ln|t|+C)=e^(ln|t|)e^C=Kt`
(We let `e^C=K`, constant)
So `x = Kt - 3`.
Typical solution and graph
We let `K = 7`, for illustration):
Typical solution graph `x=7t-3`.
Example 5
Solve `sqrt(1+4x^2)\ dy=y^3x\ dx`
Answer
Separating variables gives us:
`(dy)/y^3=(x\ dx)/(sqrt(1+4x^2))`
Integrating gives us:
`int(dy)/y^3=int(x\ dx)/(sqrt(1+4x^2)`
We now proceed to integrate the 2 sides separately. That is, we integrate the left side in y only (since after separating the variables we have terms in y and a dy on the left) and we work on the right side in x only (since we have terms in x and a dx only on the right).
For the right hand side involving x, let u = (1 + 4x2), so du = 8x dx and du/8 = x dx.
`int(dy)/y^3=1/8int(du)/sqrtu`
`=(-1)/(2y^2)`
`=1/8(2)u^(1"/"2)+K`
`=1/4sqrt(1+4x^2)+K`
So the solution is given by:
`(-1)/(2y^2)=1/4sqrt(1+4x^2)+K`
We could go on to solve this in y, as follows:
Multiply both sides by `−2`:
`1/y^2=-1/2sqrt(1+4x^2)-2K`
For convenience, introduce a new variable `K_1 = -4K`, so that we'll have `-2K=K_1/2`. Our solution becomes:
`1/y^2=-1/2sqrt(1+4x^2)+K_1/2 =` ` (K_1 - sqrt(1+4x^2))/2`
Take the reciprocal of both sides:
`y^2=2/(K_1-sqrt(1+4x^2))`
Then solve for y:
`y=(+-sqrt2)/sqrt(K_1-sqrt(1+4x^2))`
(The constant K1 can be chosen so that the expression in the denominator is real.)
Here is the graph of a typical solution for Example 5 where we have taken `K=50`:
Typical solution graph `y=(+-sqrt2)/sqrt(50-sqrt(1+4x^2))`.
Particular Solutions
Our examples so far in this section have involved some constant of integration, K.
We now move on to see particular solutions, where we know some boundary conditions and we substitute those into our general solution to give a particular solution.
Example 6
Find the particular solution for
`(dy)/(dx)+2y=6`
given that x = 0 when y = 1.
Answer
We solve as before, and then use the given information to find the value of the unknown K.
Separating variables:
`(dy)/(dx)+2y=6`
`(dy)/(dx)=6-2y`
`dy=(6-2y)dx`
`(dy)/(6-2y)=dx`
Integrating gives:
`int(dy)/(6-2y)=intdx`
`(-1)/2ln|6-2y|=x+K`
[For the integral involving `y`, we put `u = 6 - 2y` giving `du = - 2\ dy`. This means we'll replace `dy` with `(-1/2)du` and integrate `(1/u)du` giving `ln\ u`.]
Now, when `x = 0`, `y = 1`; so we have:
`(-1)/2ln|6-2(1)|=0+K`
`K=(-1)/2ln|4|`
So, on substituting this back into our previous equation and doing some algebra, we obtain:
`(-1)/2ln|6-2y|=x+(-1)/2ln|4|`
`(-1)/2[ln|6-2y|-ln 4]=x`
`ln (6-2y)/4=-2x`
Taking "`e` to both sides":
`(6-2y)/4=e^(-2x)`
`6-2y=4e^(-2x)`
`y=3-2e^(-2x)`
Checking our solution: `(dy)/(dx)=4e^(-2x)`and so
`"LHS"=(dy)/(dx)+2y`
`=4e^(-2x)+2(3-2e^(-2x))`
`=6`
`="RHS"`
Also, when `x = 0`, `y = 3 - 2e^0= 1`.
So the particular solution is given by: `y = 3 - 2e^(-2x)`
Here is the graph of our solution for Example 6:
Solution graph `y=3-2e^(-2x)`, showing the curve passing through `(0, 1)`.
Example 7
Solve
`x\ dy = y\ ln\ y\ dx`,
given
`x = 2` when `y = e`.
Answer
Separating variables:
`x\ dy=y\ ln\ y\ dx`
`(dy)/(y\ ln\ y)=(dx)/x`
Integrating: [For the y part, let u = ln y, then du = dy/y].
`int(dy)/(y\ ln\ y)=int(dx)/x`
`ln(ln\ y)=ln\ x+K`
Substituting x = 2 when y = e gives:
`ln(ln\ e)=ln\ 2+K`
`ln(1)=ln\ 2+K`
`0=ln\ 2+K`
`K=-ln\ 2`
Substituting this in our general solution:
`ln(ln\ y)=ln\ x-ln\ 2` `=ln\ x/2`
This gives us:
`ln\ y=x/2`
So the particular solution is given by:
`y=e^(x"/"2)`
Here is the graph of our solution for Example 7:
Solution graph `y=e^(x//2)`, showing the curve passes through `(2, e)`.
Example 8 - RL Circuit Application
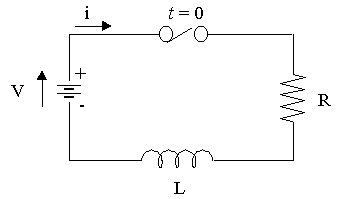
In an RL circuit, the differential equation formed using Kirchhoff's law, is
`Ri+L(di)/(dt)=V`
Solve this DE, using separation of variables, given that
R = 10 Ω, L = 3 H and V = 50 volts, and i(0) = 0.
Answer
Substituting R = 10, L = 3 and V = 50 gives:
`10i+3(di)/(dt)=50`
`3(di)/(dt)=50-10i`
First, we separate the variables.
`(di)/((50-10i))=(dt)/3`
Integrate.
`1/10int(di)/(5-i)=1/3intdt`
`-1/10ln(5-i)=t/3+K`
Since i(0) = 0,
`-1/10ln(5-0)=0+K`
`K=(-ln\ 5)/10`
So, substituting for K:
`-1/10ln(5-i)=t/3-(ln\ 5)/10`
Put log parts together.
`-t/3=1/10ln(5-i)-(ln\ 5)/10`
Multiply both sides by 10
`-(10t)/3=ln(5-i)-ln\ 5`
`-(10t)/3=ln\ (5-i)/5`
`e^(-10t"/"3)=(5-i)/5`
`5e^(-10t"/"3)=5-i`
`i=5-5e^(-10t"/"3)=5(1-e^(-10t"/"3))`
The graph shows that the current builds up and levels out at a maximum value of 5 A.
Solution graph `i=5(1-e^(-10t"/"3))`.
NOTE: We could have solved this for `i` another way. Here it is - you may find it easier.
`-1/10ln(5-i)=t/3-(ln\ 5)/10`
`ln(5-i)=-(10t)/3+ln\ 5`
Raising both sides as a power of e:
`5-i=e^(-10t"/"3 + ln\ 5)` `=e^(-10t"/"3)e^(ln\ 5)` `=5e^(-10t"/"3)`
`i=5-5e^(-10t"/"3)` `=5(1-e^(-10t"/"3))`
Example 9 - Skydiver's Terminal Velocity
When a skydiver jumps out of a (perfectly good) aeroplane, apart from experiencing sheer terror (and exhilaration), she experiences two forces:
Gravity, acting downwards
Air resistance, acting upwards
Gravity is written g and on earth its acceleration has value 9.8 ms-2.
Air resistance depends on the size and shape of the item that is dropping through the air. We use the constant k to represent the amount of air resistance. It is called the coefficient of drag.
The air resistance is proportional to the square of the velocity, so the upwards resistance force due to air resistance can be represented by
Fair = kv2.
Now the force on the object due to gravity is:
Fgravity = mg, where g is the acceleration due to gravity.
The total force acting on the body is
`F_("total") = F_("air") - F_("gravity") = kv^2 - mg`
Dividing throughout by m gives us a good model for the velocity v of an object falling through the air:
`a=k/mv^2-g`
We can write this as
`(dv)/(dt)=k/mv^2-g`
Questions
a. Find an expression for the velocity of a sky diver at time t.
b. Find the velocity after 5 seconds for a sky diver of mass m = 80 kg and k = 0.2
c. Find the terminal velocity for any object for general values of g and k.
d. Find the terminal velocity our skydiver with mass m = 80 kg and k = 0.2.
Answer
a. General Formula for Velocity of an Object Falling in Air
We rewrite our differential equation:
`(dv)/(dt)=k/mv^2-g`
in a more convenient form :
`(dv)/(dt)=g(k/(mg)v^2-1)`
Also for convenience, let c be defined as:
`c=sqrt((mg)/k`
So:
`1/c^2=k/(mg)`
We can rewrite our differential equation as:
`(dv)/(dt)=g(v^2/c^2-1)`
This is the same as:
`(dv)/(dt)=g((v^2-c^2)/c^2)`
Separating the variables:
`(c^2dv)/(v^2-c^2)=g\ dt`
Integrating both sides:
`c^2int(dv)/(v^2-c^2)=intg dt`
We multiply the fraction by `-1`, thus reversing the order of `(v^2-c^2)`, and also at the front to compensate, so the substitution step coming up later is possible. (Otherwise, we would be trying to find the log of a negative number when finding `K`.)
`-c^2int(dv)/(c^2-v^2)=int g dt`
To perform this integration, we could either:
- Factor the denominator, use partial fractions and then integrate (it needs the logarithm form), or
- Use a table of integrals (integral #13), (easier); or
- Use a computer algebra system, like Scientific Notebook. (easiest)
We integrate and obtain:
`(-c^2)1/(2c)ln((c+v)/(c-v))= g t +K`
"K" is the constant of integration.
At `t = 0`, `v = 0` and after substituting, we conclude `K = 0`. Therefore:
`-c/2ln((c+v)/(c-v))=g t`
Now we solve for v.
Multiply both sides by `-2` and divide by c:
`ln((c+v)/(c-v))=-(2g t)/c`
Take e to both sides to remove the logarithm:
`(c+v)/(c-v)=e^(-2g t"/"c)`
Multiply out and solve for v:
`c+v=(c-v)e^(-2g t"/"c)`
`c+v=ce^(-2g t"/"c)-ve^(-2g t"/"c)`
`ve^(-2g t"/"c)+v=ce^(-2g t"/"c)-c`
`v=c(e^(-2g t"/"c)-1)/(e^(-2g t"/"c)+1)`
This is the velocity of our object at time t.
b. Velocity for Particular Sky Diver at Specific Time
First, we find c for our given situation. This was the expression for c:
`c=sqrt((mg)/k)`
We use the given mass and the coefficient of drag for the skydiver.
mass = m = 80 kg
coefficient of drag = k = 0.2
So
`c=sqrt((mg)/k)`
`=sqrt((80xx9.8)/0.2)`
`=62.6`
Next, we substitute the given time value (t = 5) and c = 62.6 to find the required velocity:
`v=c(e^(-2g t"/"c)-1)/(e^(-2g t"/"c)+1)`
`=62.6(e^(-2(9.8)(5)"/"62.6)-1)/(e^(-2(9.8)(5)"/"62.6)+1)`
`=-40.9580`
The units are ms-1, so the velocity at time t = 5 s is approximately 147 km/h (1 ms-1 = 3.6 km/h), in the downward direction.
c. Terminal velocity
The expression for velocity at time t we found earlier:
`v=c(e^(-2g t"/"c)-1)/(e^(-2g t"/"c)+1)`
As t → ∞, the value of the fraction approaches −1, since e-2gt/c → 0, giving us the terminal velocity `v=-c`.
So
`c=sqrt((mg)/k)`
is the terminal velocity for the falling object (in the downward direction).
Note: We could have obtained the above expression without knowing the expression for velocity at time t, by simply noting the velocity of the object reaches terminal velocity when the acceleration is 0.
That is, solving the following acceleration expression to find the velocity:
`a=k/mv^2-g=0`
This gives terminal velocity
`v=sqrt((mg)/k)`
d. Terminal Velocity for Skydiver Example
We already found the expression for c (which is the terminal velocity) in Part (b)
`c=sqrt((mg)/k)`
`=sqrt((80xx9.8)/0.2)`
`=62.6`
So the terminal velocity is approximately 225 km/h, since 1 ms-1 = 3.6 km/h.
The graph of the velocity against time shows that it takes around 15 seconds to reach (or "get very close to") the terminal velocity:
Velocity graph `v=225(e^(-2(9.8) t"/"62.6)-1)/(e^(-2(9.8) t"/"62.6)+1)`, showing the point `(5, -147)`.
Note:
- The graph shows that the terminal velocity is never actually reached - the skydiver's velocity just gets closer and closer to that velocity.
- The graph includes the point representing the velocity at time t = 5, found earlier.
- Actually, the air resistance increases as the air gets more dense nearer the Earth's surface. We have assumed it remains constant for this problem.
- The human sky diver can change k easily by either spreading their arms and legs (which will slow them down), or diving down with arms and legs tightly together (which will increase their speed)

