8. Applications of Radian Measure
by M. Bourne
Linear velocity applet
Don't miss the interactive angular/linear velocity animation on this page.
Go to
Angular velocity applet
In this section, we see some of the common applications of radian measure, including arc length, area of a sector of a circle, and angular velocity.
Go back to the section on Radians if you are not sure what is going on.
Arc Length
The length, s, of an arc of a circle radius r subtended by θ (in radians) is given by:
s = r θ
If r is in meters, s will also be in meters. Likewise, if r is in cm, s will also be in cm.
Example 1
Find the length of the arc of a circle with radius `4\ "cm"` and central angle `5.1` radians.
Answer
We need to find length s.
s = r θ
= 4 × 5.1
= 20.4 cm
Area of a Sector
Area, A, of a sector of a circle.
The area of a sector with central angle θ (in radians) is given by:
`"Area"=(theta\ r^2)/2`
If r is measured in `"cm"`, the area will be in `"cm"`2. If r is in `"m"`, the area will be in `"m"`2.
Example 2
Find the area of the sector with radius `7\ "cm"` and central angle `2.5` radians.
Answer
This is the area we need to find:
Area, a sector of a circle, radius 7 and central angle 2.5 rad.
`"Area"=(theta\ r^2)/2=(2.5xx7^2)/2=61.25\ "cm"^2`
Angular Velocity
The time rate of change of angle θ by a rotating body is the angular velocity, written ω (omega). It is measured in radians/second.
If v is the linear velocity (in m/s) and r is the radius of the circle (in m), then
v = rω
Note: If r is in `"cm"`, v will be in `"cm/s"`.
Example 3
A bicycle with tyres `90\ "cm"` in diameter is travelling at `25` km/h. What is the angular velocity of the tyre in radians per second?
Answer
Bicycle wheel, radius 90 cm.
The arrows represent the linear speed of 25 km/h
We learned that linear velocity for a wheel rotating at ω rad/s is given by:
v = r ω
The units are a mix of cm and km. Let's present everything in meters.
We need to convert v to m/s first.
`25\ "km/h" = 25000\ "m/h"`
` = 25000/3600 "m/s"`
` = 6.94444\ "m/s"`
Also, we have
`r = (90\ "cm")/2 = 45\ "cm" = 0.45\ "m"`
So `ω = v/r = 6.94444/0.45 = 15.43\ "rad/s"`
Interactive linear velocity applet
Background
A car is going around a circular track of radius 0.5 km. The speedometer in the car shows the (magnitude) of the linear velocity.
At first, the car goes around the track once in just over 6 minutes. It's angular velocity is 1 rad/min or one complete revolution in 2π = 6.28 min.
The distance travelled in this time is the circumference of the circle, C = 2πr = 2π(0.5) = 3.14 km. So the car is travelling at `(3.14" km")/(6.28 min) = 0.5" km/min" = 30" km/h"`.
The linear velocity showing on the speedo is 30 km/h.
Things to do
In this applet, you can:
- Vary the radius of the track
- Vary the angular velocity of the car
Observe the change in linear speed as you do so.
Of course, angle measures are in radians in this applet.
r = 0 km ω = 0 rad/min
v = rω = 0 × 0 = 0 km/min = 0 km/h
Copyright © www.intmath.com Frame rate: 0
Exercises:
1. A section of side walk is a circular sector of radius `1.25\ "m"` and central angle `50.6°`. What is the area of this section of sidewalk?
Answer
Circular sector, radius 1.25 m, central angle 56°.
First we must convert `50.6°` to radians:
`50.6° = 50.6 × π/180 = 0.8831\ "radians"`
`"Area"=(theta\ r^2)/2`
`=(0.8831xx1.25^2)/2`
`=0.690\ "m"^2`
2. A cam is in the shape of a circular sector with radius `1.875\ "cm"` and central angle `165.58°`. What is the perimeter of the cam?
Answer
Circular sector, radius 1.875 cm, central angle 165.58°.
The length of the arc is given by s = rθ.
First we must convert `165.58°` into radians:
`165.58° = 165.58 × π/180 = 2.8899` radians.
So arc length is: `s = 1.875 × 2.8899 = 5.419` cm.
So the perimeter of the cam is:
`2 × 1.875 + 5.419 = 9.169` cm.
3. The roller on a computer printer makes `2200` rev/min. What is its angular velocity?
Answer
Angular velocity is:
`ω = 2200 r/min × (2π) / 60 = 230.4\ "rad/s"`.
4. The propeller on a motorboat is rotating at `130` rad/s. What is the linear velocity of a point on the tip of a blade if the blade is `22.5` cm long?
Answer
Linear velocity = v = ωr
In this example, ω = 130 rad/s and r = 0.225 m
So the linear velocity is:
v = 130 × 0.225 = 29.3 ms-1.
Note 1: ms-1 is an equivalent way of writing m/s. This comes from the index laws where the rule is `s^-1= 1/s`.
Note 2: It is common in physics to write velocity using ms-1 and the units for acceleration as ms-2.
5. The sweep second hand of a watch is `15.0` mm long. What is the linear velocity of the tip?
Answer
The second hand rotates `2pi` every minute, so per second we have:
`omega=(2pi)/60=pi/30"rad""/"s`
and `r= 0.015\ "m"`.
So
`v=omega r`
`=(pi/30)(0.015)`
` = 0.00157\ "m/s"`.
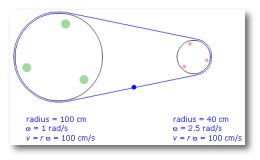
Pulley Problems
You can investigate the linear velocity of a belt moving around two pulleys in this interactive example.
Go to Pulleys simulation.