6. Trigonometric Functions of Any Angle
Think About This...
Earlier, in the section Values of Trigonometric Functions, we were given the value of a trigonometric ratio and we needed to find the angle.
The first example we did was:
Find θ, given that tan θ = 0.3462
Using our calculators, we found that θ = tan-10.3462 = 19.096o.
Now we know this is correct because tan 19.096o = 0.3462.
But also tan 199.096o = 0.3462.
Likewise, tan 379.096o = 0.3462. And some negative angles also work: tan (-160.904o) = 0.3462.
What's going on here? They all equal `0.3462`. How many answers are there?
Periodic Functions
Trigonometric functions are periodic, that is, their values re-occur over and over again. You will get a better idea of the periodic nature of trigonometric functions if you check out the chapter on Graphs of The Trigonometric Functions.
What it means is that there are many, many values of θ that will work in the equation tan θ = 0.3462. The number is infinite, actually.
Let's see what the graph of y = tan θ looks like. We see that there is a regular pattern that recurs every `180^@`. There are also "gaps" in the curve (at `90^@`, `270^@`, ...) where tan θ has no finite value. (Try it on your calculator - see what it says if you try to find the value of `tan 90^@`.)
Now, for our problem above, we can see that there are going to be an infinite number of solutions.
I have drawn a horizontal dashed line so we can see where the y-value is `0.3462`. I have then found where that horizontal line intersects the graph and dran vertical lines down to the θ axis. We see that tan 19o = 0.3462 and we can also see the other values that I suggested before:
tan 199o = 0.3462 and tan 379o = 0.3462.
For the negative angles,
tan (−160o) = 0.3462 and tan (-340o) = 0.3462
How Do we Find All these Angles?
Our problem here is to find a method so that we can find all the values of θ that will work in a given trigonometric equation. We start with the idea of the reference angle.
The Reference Angle
For any angle θ (greater than `90^@`), there is a corresponding acute angle α (alpha), called the reference angle, defined as:
Quadrant II: Written in the form θ = 180o - α
Quadrant II
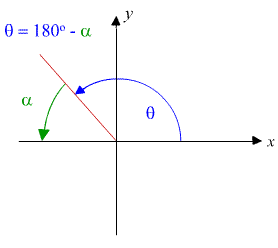
Example 1
θ = 130o = 180o - 50o
In this case, 130o is in the second quadrant and has reference angle α = 50o.
Quadrant III: Written in the form θ = 180o + α
Quadrant III
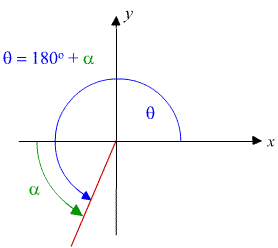
Example 2
θ = 240o = 180o + 60o
In this case, 240o is in the 3rd quadrant and the reference angle is α = 60o.
Quadrant IV: Written in the form θ = 360o - α
Quadrant IV
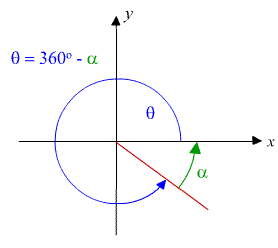
Example 3
θ = 315o = 360o - 45o
In this case, 315o is in the 4th quadrant and the reference angle is α = 45o.
Note
1. In each case,
θ is the angle of interest
α is an acute angle (that is, less than 90o)
2. We use the idea of reference angle in the following type of question.
Example 4
Find 2 angles whose cosine is `0.7`.
Answer
As we know, there are an infinite number of answers. We will find the first 2 positive angles whose cosine is `0.7`.
From our calculator, we have one answer: cos-10.7 = 45.57o.
Since this is an acute angle, we can use it as the reference angle and write α = 45.57o.
To find another answer, we remember that the 2 places where cosine is positive are the first (I) and fourth (IV) quadrants. The corresponding angle in the fourth quadrant will be:
360o − α = 360o − 45.57o = 314.43o
Check: cos 45.57o = 0.7000373 and
cos 314.43o = 0.7000373
Of course, there are an infinite number of angles where the cosine of the angle is `0.7`. Here are some of them (the values where the pink arrows are pointing):
Try the values in your calculator (eg cos 674.4o) to convince yourself that they are correct. (Your answer rounded to one decimal place should be `0.7` for each one.)
Checking your answers helps you to understand what is going on and it is great for building confidence in mathematics!
Exercises
1. Write using a positive acute angle:
a) `cos 190^@`
b) `cot 290^@`
Answer
a) cos190° = cos(180° + 10°) = −cos(10°)
[Quadrant III, so negative]
b) cot 290° = cot(360° − 70°) = −cot(70°)
[Quadrant IV, so negative]
2. Find `tan 152.4^@` [use calculator]
Answer
tan 152.4° = −0.5223
3. Find `csc\ 194.82^@` [use calculator]
Answer
`csc\ 194.82^@ = 1/(sin 194.82^@) = -3.9096`
4. Find θ if sin θ = −0.8480 (0o < θ < 360o)
Answer
We find the reference angle first.
Let sin α = 0.8480, then we have
α = arcsin 0.8480 = 58.0°
Since `sin theta` is negative, θ must be in Quadrants III or IV.
So θ = 180° + 58.0° = 238.0° or
θ = 360° − 58.0° = 302.0°
Arcsin or sin-1?
Why do I use "`arcsin`" instead of what is on your calculator, "`sin^-1`"?
- Students always get confused with `sin^-1 x` and `csc x` (they are NOT the same: `sin^-1 x` means "the angle whose `"sine"` is x", whereas `csc x` means `1/(sin x)`).
- It is standard in science and engineering to use "`arcsin`", rather than "`sin^-1`".
- Most computer programs use "`arcsin`" or "`"asin"`" for the inverse of `"sine"` - not "`sin^-1`", so it is a good idea to get used to it early on.
5. If `tan θ = -0.809` and `csc\ θ > 0`, find `cos θ`.
Answer
The only quadrant where `tan theta` is negative and `csc\ theta` is positive is the second quadrant.
First, we find the reference angle:
Let tan α = 0.809 then α = arctan 0.809 = 39.0°
So θ = 180° − 39.0° = 141.0°
So cos θ = −0.777
6. If `sec θ = 1.122` and `sin θ < 0`, find `cot θ`.
Answer
The only quadrant where `sec theta` is positive and `sin theta` is negative is Quadrant IV.
Considering the reference angle `alpha` in the first quadrant, we let `sec α = 1.122`, giving `cos alpha=1/1.122=0.8912656`.
So `alpha = arccos 0.8912656 = 27.0^@`
We now use that reference angle to find the value of `theta` in the fourth quadrant.
So ` θ = 360^@ − 27.0^@ = 333.0^@`
Finally, we find the `cot` of that fourth quadrant angle.
So `cot theta=1/(tan 333.0^@)=-1.963`