7. Ratio and Proportion

We need to be a bit careful because lots of people use the words "ratio", "fraction" and "proportion" to mean the same thing in everyday speech.

This makes it difficult when we meet the terms in mathematics, because they are not necessarily used to mean the same thing.

Ratios and Fractions

Example 1

Ethanol or methanol (wood-based methyl alcohol) is sometimes added to gasoline to reduce pollution and cost. Car engines can typically run on a petrol-ethanol mixture in a ratio of `9:1`. The "`9:1`" means that for each nine units of petrol, there is 1 unit of ethanol.

For example, if we had 9 L of petrol, we would need 1 L of ethanol.

We can see that altogether we would have 10 L of the mixture.

As fractions, the proportion of each liquid is:

`1/10` ethanol

`9/10` petrol

You can see a more advanced question involving ratios and gasoline in Applied Verbal Problems, in the algebra chapter.

Example 2

Concrete

Concrete is a mixture of gravel, sand and cement, usually in the ratio `3:2:1`.

We can see that there are 3 + 2 + 1 = 6 items altogether. As fractions, the amount of each component of the concrete is:

Gravel: `3/6=1/2`

Sand: `2/6=1/3`

Cement: `1/6`

Example 3

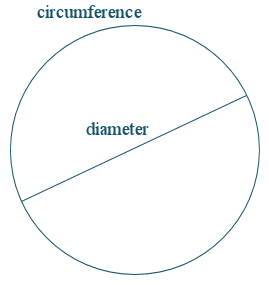
One of the most famous ratios is the ratio of the circumference of a circle to its diameter.

The value of that ratio cannot be determined exactly. It is approximately 3.141592654... We call it:

`pi` (the Greek letter "pi").

See more on Pi.

Proportion

We can talk about the proportion of one quantity compared to another.

In mathematics, we define proportion as an equation with a ratio on each side.

Example 4

Considering our ethanol/petrol example above, if we have 54 L of petrol, then we need 6 L of ethanol to give us a 9:1 mix.

We could write this as:

`54:6 = 9:1`

We could use fractions to write our proportion, as follows:

`54/6=9/1`

Rates

Example 5

A normal walking speed is 1 km in 10 min. This is a rate, where we are comparing how far we can go in a certain amount of time.

Our walking rate is equivalent to 6 km/h.

Example 6 - Conversion of Units

A bullet leaves a gun travelling at 500 m/s. Convert this speed into km/h.

Answer

A famous ratio: `Phi`

Now let's move on to an interesting ratio called `Phi` ("phi"), in Math of Beauty.