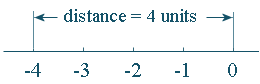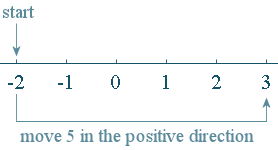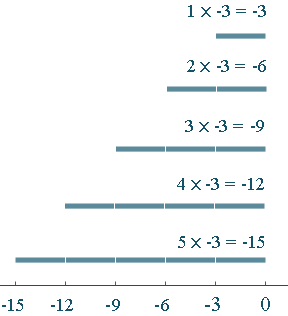1. Integers
Before we talk about integers, let’s think about the numbers we first learned as children.
On this page
Natural Numbers
The natural numbers arise from counting. We can have
no objects: 0
one object: 1
two objects: 2
... etc.
We can represent the natural numbers on a one-dimensional number line. Here is a graph of the first 4 natural numbers 0, 1, 2, and 3:
We put a dot on those numbers that are included. In this case, we have graphed 0, 1, 2, and 3, but we have not included 4 to illustrate the point.
We can also write the natural numbers as a set:
{0, 1, 2, 3, 4, ...}
The natural numbers are sometimes called whole numbers or counting numbers. There is some disagreement among mathematicians about whether or not zero should be included. [See Is 0 a Natural Number?]
Less Than and Greater Than
On the number line, LEFT is LESS. We use the "<" (less than) sign to indicate one number is smaller than another number.
So for example:
`1 < 3` (We say this as "one is less than three".)
We use the ">" (greater than) sign to indicate one number is bigger than another.
`4 > 0` (We say "four is greater than zero".)
Negative Numbers
One of the biggest problems people have in mathematics is with negative numbers. Take great care with negatives!
A negative number is any number whose value is less than zero. We write a minus in front of negative numbers.
Examples of Negative Numbers
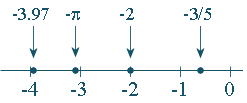
(a) ` -3.97`
(b) `-pi`
(c) `-2`
(d) `-3/5`
The negative numbers are represented on the left half of the number line. The four negative numbers above are indicated on the following number line like this:
Once again, we have put dots on the number line representing the numbers in the set.
Uses of Negative Numbers
- Temperatures (below zero)
- Bank balances which are overdrawn
- Golf ("under par" means the number of shots less than par for the golf course)
- Engineering (forces acting in different directions, for example gravity is usually written as a negative force, since upwards forces are usually regarded as positive)
- Science
Now we're ready to dive in.
Integers
Defined as:
- The negative natural numbers (...,−4, −3, −2, −1) and
- 0; and
- The positive natural numbers (1, 2, 3, 4, ...).
Notice that the set does not include decimals or fractions − just whole numbers.
They are represented on the number line like this:
Recall from above that on the number line, LEFT is LESS.
Examples of Comparing Integers
(a) −4 < 2 (we say "negative 4 is less than 2")
(b) −103 < −45
Similarly, if a number is to the RIGHT of second number, it is greater than the second number.
(c) 2 > −2 (we say "2 is greater than negative 2")
(d) 3 > −150
Absolute Value
The distance from 0 to a number is its absolute value (written using vertical line brackets around the number).
Examples of Absolute Value
(a) `|-4| = 4`
The distance from `-4` to `0` is `4` units:
Similarly:
(b) `|3|=3`
(c) `|-12.85| = 12.85`
In each example, the number on the right is the distance from 0.
Opposite of an Integer
The opposite of an integer is obtained by changing its sign. (That is, change − to + or change + to −).
Examples of Opposite of an Integer
(a) The opposite of `-3` is `3` and
(b) The opposite of `4` is ` -4`.
Notice that opposite is not the same as absolute value.
Integer Addition
Use the number line and think of "journeys".
Examples of Integer Addition
(a) ` -2 + 5` means "start at `-2` and go `5` in the positive direction"
So we have:
Our answer is:
`-2 + 5 = 3`
Similarly
(b) `3 + -7` means "start at `3` and go `7` in the negative direction".
Our answer is: `3 + -7 = -4`
(c) ` -5 + 12` means "start at ` -5` and go `12` in the positive direction"
The answer is ` -5 + 12 = 7`
Practical Example of Integer Addition
It is -4° and snowing. The forecast for tomorrow is for a rise in temperature of 6°. What will it be tomorrow?
Answer: `-4 + 6 = 2`. It will be 2° tomorrow.
Integer Subtraction
We can change the subtraction into a more familiar addition by realising that subtracting an integer is the same as adding its opposite.
Examples of Integer Subtraction
(a) ` -4 - (-3) = -4 + (+3) = -1 `
(We added +3 because the opposite of -3 is +3.)
(b) `5 - (+7) = 5 + (-7) = -2.`
(We added -7 because the opposite of +7 is -7. Eventually you’ll see the question is the same as "5 - 7" and we can do this as a journey: Start at 5 and move 7 units to the left. Answer: -2.)
Integer Multiplication
When multiplying integers, we can think of multiplying "blocks" of negative numbers.
Examples of Integer Multiplication
(a) Here is an integer times an integer:
`5 xx -3 = -15`
Why is this so? We are simply taking "5 lots of −3", like this:
Notice that we were multiplying a positive number by a negative number and our result was negative.
Similarly, we can show:
(b) ` -6 xx 2 = -12` (negative times positive gives negative)
and
(c) `-3 xx -7 = 21` (multiplying 2 negatives gives a positive)
Practical example of Integer Multiplication
The acceleration due to gravity (1 g) on the earth is about −10 ms−2. (It’s negative because it acts downwards. This is a convention.)
On the planet Jupiter, the acceleration due to gravity is 2.65 times the acceleration due to gravity on the Earth.
On Jupiter, the acceleration is around:
`2.65 xx -10 "ms"^-2 ~~ -26.5\ "ms"^-2`
Summary
We can summarise the results for multiplying:
positive × positive = positive
+ × + = +
Signs the same: positive answer
Example: 2 × 3 = 6
negative × positive = negative
− × + = −
Signs different: negative answer
Example: −8 × 2 = −16
positive × negative = negative
+ × − = −
Signs different: negative answer
Example: 5 × −2 = −10
negative × negative = positive
− × − = +
Signs the same: positive answer
Example: −5 × −3 = 15
Challenge: Integer Multiplication
What is a practical application for −3 × −7 = 21?
Answer
If it is 0° now and the temperature is dropping 3° per hour, what was the temperature 7 hours ago?
Integer Division
When we divide with negative numbers, we have similar results to those for multiplication:
positive ÷ positive = positive
+ ÷ + = +
Signs the same: positive answer
Example: 15 ÷ 3 = 5
negative ÷ positive = negative
− ÷ + = −
Signs different: negative answer
Example: −8 ÷ 2 = −4
positive ÷ negative = negative
+ ÷ − = −
Signs different: negative answer
Example: 21 ÷ −7 = −3
negative ÷ negative = positive
− ÷ − = +
Signs the same: positive answer
Example: −50 ÷ −5 = 10
We can rewrite division problems as multiplication problems, as in the following example.
Example of Integer Division
−32 ÷ 4
is the same question as
4 × what? = −32
Challenge: Integer Division
What is a practical application for −10 ÷ 5 = −2?
Answer
In financial accounting, a loss of $10 million could be written as -$10 million.
If we make a loss of $10 million in 5 years, then the average rate of loss is
−10 ÷ 5 = −2,
or −$2 million per year.
(Similar, but for the sporty among you:) In golf, "1 under par" means that you get the ball in the hole in one stroke less than expected for that hole.
So your score may be 10 under par after 5 holes of golf. Your average per hole is
−10 ÷ 5 = −2,
or 2 under par per hole.
Integer Properties
The set of integers is closed, commutative, associative and has an identity under both addition and multiplication.
The following table gives examples and explains what this means in plain English.
| Addition | Multiplication | |
|---|---|---|
| Closed |
3 + −7 = −4 When we add 2 integers, we get an integer. |
−5 × −3 = 15 When we multiply 2 integers, we get an integer. |
| Commutative |
4 + −5 = −5 + 4 It doesn’t matter what order we add integers, we get the same answer. |
2 × −5 = −5 × 2 It doesn’t matter what order we multiply integers, we get the same answer. |
| Associative |
(4 + −2) + −5 = 4 + (−2 + −5) When adding 3 integers, it doesn’t matter if we start by adding the first pair or the last pair; the answer is the same. |
(4 × −2) × −5 = 4 × (−2 × −5) When multiplying 3 integers, it doesn’t matter if we start by multiplying the first pair or the last pair; the answer is the same. |
| Identity |
−5 + 0 = 0 + −5 = −5 Zero is the identity element for addition. By adding zero on either side, we don’t change the number. |
−3 × 1 = 1 × −3 = −3 One is the identity element for multiplication. By multiplying by 1 on either side, we don’t change the number. |
The Distributive Law over addition and subtraction holds for integers:
| Addition | Subtraction | |
|---|---|---|
| Distributive |
3(2 + −4) We multiply each number inside the brackets by the number outside, retaining the plus in the middle. |
−2(5 − 7) We multiply each number inside the brackets by the number outside, retaining the minus in the middle. |
Game
Magic Square
In a magic square, all the rows, all the columns and the 2 diagonals must add to the same number.
1. Complete the magic square, using only the positive integers 1 to 9:
1 4 9 2
Answer
Answer
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
2. Complete the magic square, using only the integers:
−10, −8, −6, −4, 0, 2, 4, 6
−2
Answer
Answer
| 4 | −10 | 0 |
| −6 | −2 | 2 |
| −4 | 6 | −8 |