6. Matrices and Linear Equations
by M. Bourne
We wish to solve the system of simultaneous linear equations using matrices:
a1x + b1y = c1
a2x + b2y = c2
If we let
`A=((a_1,b_1),(a_2,b_2))`, `\ X=((x),(y))\ ` and `\ C=((c_1),(c_2))`
then `AX=C`. (We first saw this in Multiplication of Matrices).
If we now multiply each side of
AX = C
on the left by
A-1, we have:
A-1AX = A-1C.
However, we know that A-1A = I, the Identity matrix. So we obtain
IX = A-1C.
But IX = X, so the solution to the system of equations is given by:
X = A-1C
See the box at the top of Inverse of a Matrix for more explanation about why this works.
Note: We cannot reverse the order of multiplication and use CA-1 because matrix multiplication is not commutative.
Example - solving a system using the Inverse Matrix
Solve the system using matrices.
−x + 5y = 4
2x + 5y = −2
Always check your solutions!
Answer
We have:
`A=((-1,5),(2,5)),` ` \ X=((x),(y))\ ` and `\ C=((4),(-2))`
To solve the system, we need the inverse of A, which we write as A-1.
Swap leading diagonal:
`((5,5),(2,-1))`
Change signs of the other 2 elements:
`((5,-5),(-2,-1))`
Now we find the determinant of A:
`|A| = -5 - 10 = -15`
So
`A^-1` `=-1/15((5,-5),(-2,-1))` ` = ((-1/3,1/3),(2/15,1/15))` ` = ((-0.333,0.333),(0.133,0.067)) `
So the solution to the system is given by:
`X=A^-1C` `=((-0.333,0.333),(0.133,0.067))((4),(-2))` `=((-2),(0.4)) `
This answer means that we have found the solution `x = -2` and `y = 0.4`.
Is the solution correct?
We check it in the original set of equations:
`{:(-x+5y,=4),(2x+5y,=-2):}`
Substituting `x = -2` and `y = 0.4`, we get:
`−(−2) + 5×(0.4) = 2 + 2 = 4` [Checks OK]
`2×(−2) + 5×(0.4)` ` = −4 + 2` ` = −2` [Checks OK]
So the solution to the original system of equations is
`x = -2,\ \ y = 0.4`.
Solving 3×3 Systems of Equations
We can extend the above method to systems of any size. We cannot use the same method for finding inverses of matrices bigger than 2×2.
We will use a Computer Algebra System to find inverses larger than 2×2.
Example - 3×3 System of Equations
Solve the system using matrix methods.
`{: (x+2y-z=6),(3x+5y-z=2),(-2x-y-2z=4) :}`
Did I mention? It's a good idea to always check your solutions.
Answer
`A=((1,2,-1),(3,5,-1),(-2,-1,-2)),` `X=((x),(y),(z)),` and `C=((6),(2),(4))`
Using Scientific Notebook, we find the inverse of A to be:
`A^-1=((5.5,-2.5,-1.5),(-4,2,1),(-3.5,1.5,0.5))`
(We could have used Gauss-Jordan Elimination if we need to show all steps.)
So the solution to the system of equations is:
`X=A^-1C`
`=((5.5,-2.5,-1.5),(-4,2,1),(-3.5,1.5,0.5))((6),(2),(4))`
`=((22),(-16),(-16))`
Check:
`22 + 2(-16) - (-16) = 6` [Checks OK]
`3(22) + 5(-16) - (-16) = 2` [Checks OK]
`-2(22) - (16) - 2(-16) = 4` [Checks OK]
So the solution is `x = 22`, `y = -16` and `z = -16`.
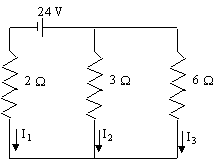
Example - Electronics application of 3×3 System of Equations
Find the electric currents shown by solving the matrix equation (obtained using Kirchhoff's Law) arising from this circuit:
`((I_1+I_2+I_3),(-2I_1+3I_2),(-3I_2+6I_3))=((0),(24),(0))`
(You can explore what the solution for this example really means in this 3D interactive systems of equations applet.)
Answer
We can write this as:
`((1,1,1),(-2,3,0),(0,-3,6))((I_1),(I_2),(I_3))=((0),(24),(0))`
So we have:
`((I_1),(I_2),(I_3))=((1,1,1),(-2,3,0),(0,-3,6))^-1((0),(24),(0))`
Using a computer algebra system to perform the inverse and multiply by the constant matrix, we get:
`I_1= -6\ "A"`
`I_2= 4\ "A"`
`I_3= 2\ "A"`
We observe that I1 is negative, as expected from the circuit diagram.
Exercise 1
The following equations are found in a particular electrical circuit. Find the currents using matrix methods.
`{: (I_A+I_B+I_C=0),(2I_A-5I_B=6),(5I_B-I_C=-3) :}`
(This example is also included in the 3D interactive systems of equations applet.)
Answer
We need to form the matrices:
`A=((1,1,1),(2,-5,0),(0,5,-1))`, `\ X=((I_A),(I_B),(I_C))\ ` and `\ C=((0),(6),(-3))`
Using Scientific Notebook (or any Computer Algebra System), we find:
`A^-1` ` = ((0.294,0.353,0.294),(0.118,-0.059,0.118),(0.588,-0.294,-0.412))`
and so (continuing to use Scientific Notebook, with rounding to 3 decimal places):
`((I_A),(I_B),(I_C))=A^-1C`
`=((0.294,0.353,0.294),(0.118,-0.059,0.118),(0.588,-0.294,-0.412))((0),(6),(-3))`
`=((1.236),(-0.708),(-0.528))`
Therefore
`I_A= 1.236\ "A"`,
`I_B= -0.708\ "A"` and
`I_C= -0.528\ "A"`
Exercise 2
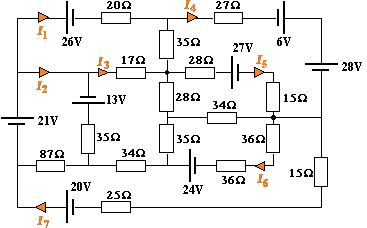
Recall this problem from before? If we know the simultaneous equations involved, we will be able to solve the system using inverse matrices on a computer.
The circuit equations, using Kirchhoff's Law:
−26 = 72I1 − 17I3 − 35I4
34 = 122I2 − 35I3 − 87I7
−4 = 233I7 − 87I2 − 34I3 − 72I6
−13 = 149I3 − 17I1 − 35I2 − 28I5 − 35I6 − 34I7
−27 = 105I5 − 28I3 − 43I4 − 34I6
24 = 141I6 − 35I3 − 34I5 − 72I7
5 = 105I4 − 35I1 − 43I5
What are the individual currents, I1 to I7?
Phone users

NOTE: If you're on a phone, you can scroll any wide matrices on this page to the right or left to see the whole expression.
Answer
Solving currents in a Circuit (7 × 7 system)
We solve this using a computer as follows. We just write the coefficient matrix on the left, find the inverse (raise the matrix to the power -1) and multiply the result by the constant matrix.
You can use Matlab, Mathcad or similar math software to do this. Wolfram|Alpha is a free alternative.
`X=[(72,0,-17,-35,0,0,0), (0,122,-35,0,0,0,-87), (0,-87,-34,0,0,-72,233), (-17,-35,149,0,-28,-35,-34), (0,0,-28,-43,105,-34,0), (0,0,-35,0,-34,141,-72), (-35,0,0,105,-43,0,0)]^-1 [(-26),(34),(-4),(-13),(-27),(24),(5)]`
`=[(-0.46801),(0.42932),(5.193xx10^-3),(-0.22243),(-0.27848),(0.21115),(0.20914)]`
The answer means that the currents in this circuit are (to 4 decimal places):
`I_1 = -0.4680\ "A"`
`I_2= 0.4293\ "A"`
`I_3= 0.0005\ "A"`
`I_4= -0.2224\ "A"`
`I_5= -0.2785\ "A"`
`I_6= 0.2112 \ "A"`
`I_7= 0.2091 \ "A"`
Exercise 3
We want 10 L of gasoline containing 2% additive. We have drums of the following:
Gasoline without additive
Gasoline with 5% additive
Gasoline with 6% additive
We need to use 4 times as much pure gasoline as 5% additive gasoline. How much of each is needed?
Always check your solutions!
Answer
Let
x = no. of litres of pure gasoline
y = no. of litres of 5% gasoline
z = no. of litres of 6% gasoline
From the first sentence, we have:
`x + y + z = 10`
The second sentence gives us:
We get NO additive from the pure gasoline.
We get (5% of y) L of additive from the second drum.
We get (6% of z) L of additive from the third drum.
We NEED 2% of 10 L of additive = 0.2 L = 200 mL.
So
`0.05y + 0.06z = 0.2`
Multiplying through by 100 gives us:
`5y + 6z = 20`
The second last sentence gives us:
`x = 4y`
We can write this as:
`x - 4y = 0`
This gives us the set of simultaneous equations:
x + y + z = 10
5y + 6z = 20
x − 4y = 0
So
`A=((1,1,1),(0,5,6),(1,-4,0))`, `\ C=((10),(20),(0))`
Using Scientific Notebook for the inverse:
`((1,1,1),(0,5,6),(1,-4,0))^-1` `=((0.96,-0.16,0.04),(0.24,-0.04,-0.24),(-0.2,0.2,0.2))`
Multiplying the inverse by matrix C:
`((0.96,-0.16,0.04),(0.24,-0.04,-0.24),(-0.2,0.2,0.2))((10),(20),(0))` `=((6.4),(1.6),(2))`
So we have `6.4` L of pure gasoline, `1.6` L of 5% additive and `2` L of 6% additive.
Is it correct?
`6.4 + 1.6 + 2 = 10` L [Checks OK]
`5% xx 1.6 + 6% xx 2 = 200` mL [Checks OK]
`4 × 1.6 = 6.4` [Checks OK]
Exercise 4
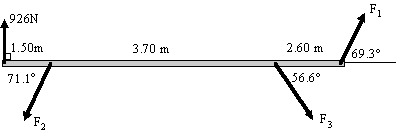
This statics problem was presented earlier in Section 3: Matrices.
From the diagram, we obtain the following equations (these equations come from statics theory):
Vertical forces:
F1 sin 69.3° − F2 sin 71.1° − F3 sin 56.6° + 926 = 0
Horizontal forces:
F1 cos 69.3° − F2 cos 71.1° + F3 cos 56.6° = 0
Moments:
7.80 F1 sin 69.3° − 1.50 F2 sin 71.1° − 5.20 F3 sin 56.6° = 0
Using matrices, find the forces F1, F2 and F3.
Answer
We write the first equation so that the constant term is on the right hand side:
F1 sin 69.3° − F2 sin 71.1° − F3 sin 56.6° = −926
In matrix form, we write the equations as:
`((sin 69.3°,-sin 71.1°,-sin 56.6°),(cos 69.3°,-cos 71.1°,cos 56.6°),(7.80 sin 69.3°,-1.50 sin 71.1°,-5.20 sin 56.6°))((F_1),(F_2),(F_3))`
`=((-926),(0),(0))`
So the solution for the system is:
`((F_1),(F_2),(F_3))=((sin 69.3°,-sin 71.1°,-sin 56.6°),(cos 69.3°,-cos 71.1°,cos 56.6°),(7.80 sin 69.3°,-1.50 sin 71.1°,-5.20 sin 56.6°))^-1((-926),(0),(0))`
`=((425.5),(1079.9),(362.2))`
So
`F_1= 425.5\ "N"`
`F_2= 1079.9\ "N"`
`F_3= 362.2\ "N"`
This is very easy and quick in Scientific Notebook, Matlab or any other computer algebra system!