1. Determinants

by M. Bourne

Before we see how to use a matrix to solve a set of simultaneous equations, we learn about determinants.

A determinant is a square array of numbers (written within a pair of vertical lines) which represents a certain sum of products.

Below is an example of a 3 × 3 determinant (it has 3 rows and 3 columns).

`|(10,0,-3),(-2,-4,1),(3,0,2)|`

The result of multiplying out, then simplifying the elements of a determinant is a single number (a scalar quantity).

Calculating a 2 × 2 Determinant

In general, we find the value of a 2 × 2 determinant with elements a, b, c, d as follows:

`|(a,b),(c,d)|=ad-cb`

We multiply the diagonals (top left × bottom right first), then subtract.

Example 1

`|(4,1),(2,3)|`

`=4xx3-2xx1`

` =12-2`

` = 10`

The final result is a single number.

We will see how to expand a 3 × 3 determinant below.

Using Determinants to Solve Systems of Equations

We can solve a system of equations using determinants, but it becomes very tedious for large systems. We will only do 2 × 2 and 3 × 3 systems using determinants.

Cramer's Rule

The solution (x, y) of the system

`a_1x+b_1y=c_1`

`a_2x+b_2y=c_2`

can be found using determinants:

`x=|(c_1,b_1),(c_2,b_2)|/|(a_1,b_1),(a_2,b_2)|`

`y=|(a_1,c_1),(a_2,c_2)|/|(a_1,b_1),(a_2,b_2)|`

Example 2

Solve the system using Cramer's Rule:

x − 3y = 6

2x + 3y = 3

Answer

3 × 3 Determinants

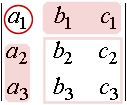
A 3 × 3 determinant

`|(a_1, b_1,c_1),(a_2,b_2,c_2),(a_3,b_3,c_3)|`

can be evaluated in various ways.

We will use the method called "expansion by minors". But first, we need a definition.

Cofactors

The 2 × 2 determinant

`|(b_2,c_2),(b_3,c_3)|`

is called the cofactor of a₁ for the 3 × 3 determinant:

`|(a_1, b_1,c_1),(a_2,b_2,c_2),(a_3,b_3,c_3)|`

The cofactor is formed from the elements that are not in the same row as a₁ and not in the same column as a₁.

Similarly, the determinant

`|(b_1,c_1),(b_3,c_3)|`

is called the cofactor of a₂. It is formed from the elements not in the same row as a₂ and not in the same column as a₂.

We continue the pattern for the cofactor of a₃.

Expansion by Minors

We evaluate our 3 × 3 determinant using expansion by minors. This involves multiplying the elements in the first column of the determinant by the cofactors of those elements. We subtract the middle product and add the final product.

`|(a_1, b_1,c_1),(a_2,b_2,c_2),(a_3,b_3,c_3)|` `=a_1|(b_2,c_2),(b_3,c_3)|` `-a_2|(b_1,c_1),(b_3,c_3)|` `+a_3|(b_1,c_1),(b_2,c_2)|`

Note that we are working down the first column and multiplying by the cofactor of each element.

Example 3

Evaluate

`|(-2,3,-1),(5,-1,4),(4,-8,2)|`

(You can explore what this example is really asking in this 3D interactive systems of equations applet.)

Answer

Cramer's Rule to Solve 3 × 3 Systems of Linear Equations

We can solve the general system of equations,

a₁x + b₁y + c₁z = d₁

a₂x + b₂y + c₂z = d₂

a₃x + b₃y + c₃z = d₃

by using the determinants:

`x=|(d_1, b_1,c_1),(d_2,b_2,c_2),(d_3,b_3,c_3)|/Delta`

`y=|(a_1, d_1,c_1),(a_2,d_2,c_2),(a_3,d_3,c_3)|/Delta`

`z=|(a_1, b_1,d_1),(a_2,b_2,d_2),(a_3,b_3,d_3)|/Delta`

where

`Delta=|(a_1, b_1,c_1),(a_2,b_2,c_2),(a_3,b_3,c_3)|`

Example 4

Solve, using Cramer's Rule:

2x + 3y + z = 2

−x + 2y + 3z = −1

−3x − 3y + z = 0

Answer

Determinant Exercises

1. Evaluate by expansion of minors:

`|(10,0,-3),(-2,-4,1),(3,0,2)|`

Answer

2. Solve the system by use of determinants:

x + 3y + z = 4

2x − 6y − 3z = 10

4x − 9y + 3z = 4

Answer