IntMath forum | Kinematics (velocity & acceleration graphs)
time/speed graph [Solved!]
Swalay 11 Sep 2016, 12:06
My question
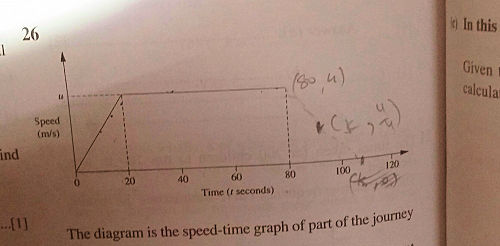
In the following time/speed graph, the horizontal line shows the time taken by a car and the vertical axis shows the speed (u cms/sec).
if D is the distance travelled from the start for 20 seconds, find t for 2D.
Relevant page
1. Velocity (s-t) Graphs
What I've done so far
Please confirm that the answer is correct.
workings: D = 1/2 x u x 20
= 10u
2D = 10u x 2
= 20u
TTaken = 20u/u
=20 secs
X
In the following time/speed graph, the horizontal line shows the time taken by a car and the vertical axis shows the speed (u cms/sec).
if D is the distance travelled from the start for 20 seconds, find t for 2D.
<img src="/forum/uploads/imf-0544-kinetics2.jpg" width="500" height="246" alt="series-binomial-theorem" />
Relevant page
<a href="/kinematics/1-velocity-graphs.php">1. Velocity (s-t) Graphs</a>
What I've done so far
Please confirm that the answer is correct.
workings: D = 1/2 x u x 20
= 10u
2D = 10u x 2
= 20u
TTaken = 20u/u
=20 secsRe: time/speed graph
Murray 11 Sep 2016, 22:13
Swalay
You are encouraged to use the Math entry system for this forum so your math is nicely aligned, and looks like mathematics.
For example your first line would look like: `D = 1/2 xx u xx 20`
Your first 4 lines are correct.
Suggestions:
(1) It's OK to introduce your own variables, but make sure you answer what the question asks for (which is `t` in this case).
(2) Think about the big picture first. If it took the car 20 seconds to travel `D` cm (while accelerating from rest), will it take another 20 s to travel the same distance?
X
Swalay
You are encouraged to use the <a href="http://www.intmath.com/forum/entering-math-graphs-images-41/how-to-enter-math:91">Math entry system</a> for this forum so your math is nicely aligned, and looks like mathematics.
For example your first line would look like: `D = 1/2 xx u xx 20`
Your first 4 lines are correct.
Suggestions:
(1) It's OK to introduce your own variables, but make sure you answer what the question asks for (which is `t` in this case).
(2) Think about the big picture first. If it took the car 20 seconds to travel `D` cm (while accelerating from rest), will it take another 20 s to travel the same distance?
Re: time/speed graph
Swalay 12 Sep 2016, 12:16
No. It will take lesser time according to me.
If speed is not constant and acceleration is not zero, less time is needed to cover the same distance after acceleration = 0
X
No. It will take lesser time according to me.
If speed is not constant and acceleration is not zero, less time is needed to cover the same distance after acceleration = 0
Re: time/speed graph
Murray 12 Sep 2016, 23:01
Correct - but your answer says (I think) that the 2nd part of the journey takes 20 seconds (which is the same as the first part), so there is an inconsistency.
Hint: to see what's going on, you could try a reasonable numerical value for u (say 1000, which is equivalent to about 38 km/h). Often it's easier to work with numbers than algebra.
X
Correct - but your answer says (I think) that the 2nd part of the journey takes 20 seconds (which is the same as the first part), so there is an inconsistency.
<b>Hint:</b> to see what's going on, you could try a reasonable numerical value for u (say 1000, which is equivalent to about 38 km/h). Often it's easier to work with numbers than algebra.
Re: time/speed graph
Swalay 16 Sep 2016, 15:12
If 2D = 20u this is the total distance travelled for the first part of the question.
Time taken for the first D = 20 secs (its includes acceleration)
Time taken for the second D < 20 secs (there is no acceleration)but now I cannot proceed.
X
If 2D = 20u this is the total distance travelled for the first part of the question.
Time taken for the first D = 20 secs (its includes acceleration)
Time taken for the second D < 20 secs (there is no acceleration)but now I cannot proceed.
Re: time/speed graph
Murray 16 Sep 2016, 22:06
I can't see where you have tried what I suggested.
Often we can't see what's going on when just using algebra. Try a real number for `u` (1000, say) first to get a sense of the situation.
This is what I mean:
First part of the journey (first 20 seconds):
`D=10u=10,000 "cm"`
Now, the second part of the journey also needs to be `D=10,000 "cm"` long. But we are now going at `u=1000 "cm/s"`, so how many seconds will that second part take?
X
I can't see where you have tried what I suggested.
Often we can't see what's going on when just using algebra. Try a real number for `u` (1000, say) first to get a sense of the situation.
This is what I mean:
First part of the journey (first 20 seconds):
`D=10u=10,000 "cm"`
Now, the second part of the journey also needs to be `D=10,000 "cm"` long. But we are now going at `u=1000 "cm/s"`, so how many seconds will that second part take?
Re: time/speed graph
Swalay 17 Sep 2016, 15:59
Time taken is Distance divided by speed
where D = 10,000 and speed is U = 1000cm/s
So that time taken = 10 secs
Therefore time taken from the start (that is from t = 0) is 20secs + 10 secs= 30 secs
X
Time taken is Distance divided by speed
where D = 10,000 and speed is U = 1000cm/s
So that time taken = 10 secs
Therefore time taken from the start (that is from t = 0) is 20secs + 10 secs= 30 secs
Re: time/speed graph
Swalay 17 Sep 2016, 18:40
The second part of the answer as to when the car will stop, this I know.
Please confirm the result so far.
X
The second part of the answer as to when the car will stop, this I know.
Please confirm the result so far.
Re: time/speed graph
Murray 18 Sep 2016, 02:40
Yes, your answer is correct for our "pretend" value of `u`.
Now you just need to express it algebraically, using `u` only.
X
Yes, your answer is correct for our "pretend" value of `u`.
Now you just need to express it algebraically, using `u` only.
Re: time/speed graph
Swalay 18 Sep 2016, 16:04
Thank you very much for your patience with me in this question.
X
Thank you very much for your patience with me in this question.
Re: time/speed graph
Murray 18 Sep 2016, 20:17
You're welcome.
But I can't see that you have completed the question (using `u`).
I meant something like this:
Journey part 1
Distance travelled `= D = 1/2 xx u xx 20 = 10u`
Time taken `= 20"s"`
Journey part 2
Distance travelled `=D=10u`
Time taken `=(10u)/u = 10 "s"`
So `t = 20 + 10 = 30 "s"`.
Always directly address the given question, using the original variables!
X
You're welcome.
But I can't see that you have completed the question (using `u`).
I meant something like this:
<b>Journey part 1</b>
Distance travelled `= D = 1/2 xx u xx 20 = 10u`
Time taken `= 20"s"`
<b>Journey part 2</b>
Distance travelled `=D=10u`
Time taken `=(10u)/u = 10 "s"`
So `t = 20 + 10 = 30 "s"`.
Always directly address the given question, using the original variables!
Related Kinematics questions
- Labeling of axes [Solved!]
On your displacement-time graph, it is more correct to title the vertical axis "position". From... Ewen 26 Nov 2015, 08:24
Kinematics lessons on IntMath
top
