IntMath forum | Differentiation - Introduction
How to differentiate? [Solved!]
Oscar 19 Dec 2015, 00:18
My question
Given: `x^3+x^2y+y^2 = 292`
Find: `dy/dx`, where : `x=600`, `y= 200`
Relevant page
7c. Given dy/dx, find y = f(x)
What I've done so far
Watched the videos and read some of the pages. But I'm lost
X
Given: `x^3+x^2y+y^2 = 292`
Find: `dy/dx`, where : `x=600`, `y= 200`
Relevant page
<a href="/integration/integration-mini-lecture-find-y-given-dy-dx.php">7c. Given dy/dx, find y = f(x)</a>
What I've done so far
Watched the videos and read some of the pages. But I'm lost
Re: How to differentiate?
Newton 19 Dec 2015, 22:20
Hi Oscar
There are examples similar to your question on this Implicit Differentiation page:
8. Differentiation of Implicit Functions
Is that enough to get you started?
Post your solution so we can see how you went. I encourage you to use the math entry system to make your math easier to read.
X
Hi Oscar
There are examples similar to your question on this Implicit Differentiation page:
<a href="/differentiation/8-derivative-implicit-function.php">8. Differentiation of Implicit Functions</a>
Is that enough to get you started?
Post your solution so we can see how you went. I encourage you to use the math entry system to make your math easier to read.
Re: How to differentiate?
Oscar 20 Dec 2015, 11:09
Yah - I can see it's like your examples.
`x^3+x^2y+y^2 = 292`
`3x^2 + x^2dy/dx + y(2x) + 2ydy/dx = 0`
`3x^2 + 2xy + (x^2 + 2y)dy/dx = 0`
`dy/dx = (3x^2 + 2xy)/(x^2 + 2y)`
Now substituting `x=600` and `y=200`
`dy/dx = (3(600)^2 + 2(600)(200))/((600)^2 + 2(200))`
`=3.66`
X
Yah - I can see it's like your examples.
`x^3+x^2y+y^2 = 292`
`3x^2 + x^2dy/dx + y(2x) + 2ydy/dx = 0`
`3x^2 + 2xy + (x^2 + 2y)dy/dx = 0`
`dy/dx = (3x^2 + 2xy)/(x^2 + 2y)`
Now substituting `x=600` and `y=200`
`dy/dx = (3(600)^2 + 2(600)(200))/((600)^2 + 2(200))`
`=3.66`
Re: How to differentiate?
Murray 20 Dec 2015, 23:33
You almost got it right - your `dy/dx` is missing a negative...
X
You almost got it right - your `dy/dx` is missing a negative...
Re: How to differentiate?
Oscar 22 Dec 2015, 01:58
Doh
Should have been:
`dy/dx = -(3x^2 + 2xy)/(x^2 + 2y)`
`dy/dx = -(3(600)^2 + 2(600)(200))/((600)^2 + 2(200))`
`=-3.66`
Thanks a lot.
X
Doh
Should have been:
`dy/dx = -(3x^2 + 2xy)/(x^2 + 2y)`
`dy/dx = -(3(600)^2 + 2(600)(200))/((600)^2 + 2(200))`
`=-3.66`
Thanks a lot.
Re: How to differentiate?
Murray 23 Dec 2015, 00:03
For interest just now, I graphed your implicit function and noticed a problem.
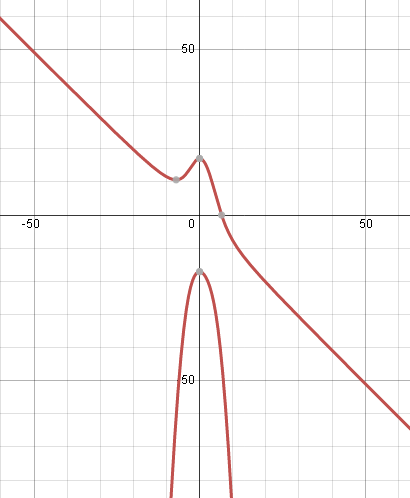
The graph doesn't even go through the point `(600, 200)`!
This is a case where we can calculate an answer, but it doesn't have any meaning.
As you can see, the graph as `x` gets very big (and goes off in the negative direction) has slope very close to `-1`.
When we substitute `x=200` into the original equation, we get `y^2+40000y+7999708 = 0` and this has solutions `y=-39799` or `y=-201.0`.
The slope is steeply negative for the first one, and very close to `-1` for the second.
Graphs tell us a lot about what is going on!
X
For interest just now, I graphed your implicit function and noticed a problem.
<img src="/forum/uploads/imf-4548-x3x2yy2is292-graph.png" width="410" height="498" alt="How to differentiate?" />
The graph doesn't even go through the point `(600, 200)`!
This is a case where we can calculate an answer, but it doesn't have any meaning.
As you can see, the graph as `x` gets very big (and goes off in the negative direction) has slope very close to `-1`.
When we substitute `x=200` into the original equation, we get `y^2+40000y+7999708 = 0` and this has solutions `y=-39799` or `y=-201.0`.
The slope is steeply negative for the first one, and very close to `-1` for the second.
Graphs tell us a lot about what is going on!
Re: How to differentiate?
Oscar 23 Dec 2015, 12:03
Thanks! I'll tell my teacher :-)
X
Thanks! I'll tell my teacher :-)
Related Differentiation - Introduction questions
- Can we find the derivative of all functions? [Solved!]
I have a silly question: Is there any function that we can't find the derivative... Garrett20 25 Dec 2015, 01:49
- Rate of change [Solved!]
Write down the rate of change of the function
f (x) = x2 between x=1, and... Rismiya 18 Dec 2015, 09:58
Differentiation - Introduction lessons on IntMath
top
