IntMath forum | Applications of Differentiation
Proof of equation [Solved!]
Hasham 16 Nov 2015, 14:08
My question
hi,
i need the proof of the following equation:
y = (4Rx(L-2x)) / L^2
I shall be very thankful to you.
Relevant page
Applications of Differentiation
What I've done so far
Tried to work out the proof, but couldn't
X
hi,
i need the proof of the following equation:
y = (4Rx(L-2x)) / L^2
I shall be very thankful to you.
Relevant page
<a href="/applications-differentiation/applications-of-differentiation-intro.php">Applications of Differentiation</a>
What I've done so far
Tried to work out the proof, but couldn't
Re: Proof of equation
Newton 16 Nov 2015, 22:57
Hello Hasham
But there is nothing to "prove" in the equation you wrote?
X
Hello Hasham
But there is nothing to "prove" in the equation you wrote?
Re: Proof of equation
Hasham 17 Nov 2015, 22:07
hi,
actualy i wanted to know the procedure of the proof of that equation.
X
hi,
actualy i wanted to know the procedure of the proof of that equation.
Re: Proof of equation
Newton 18 Nov 2015, 19:08
Hi again Hasham
Like all mathematics equations, you need to state the situation and the meaning of each of the variables.
What does `y` represent here? What are `R` and `L`?
Let me know these and I may be able to help you.
X
Hi again Hasham
Like all mathematics equations, you need to state the situation and the meaning of each of the variables.
What does `y` represent here? What are `R` and `L`?
Let me know these and I may be able to help you.
Re: Proof of equation
Hasham 19 Nov 2015, 16:40
hi, here is the information:
y= length of parabola of a structure
R = vertical distance b/w highest point if parabola and supports
L = length of span lets say of a bridge
x= x coordinate of any point
basicaly the equation is to find out the length of a parabola lets say of a bridge or something.
X
hi, here is the information:
y= length of parabola of a structure
R = vertical distance b/w highest point if parabola and supports
L = length of span lets say of a bridge
x= x coordinate of any point
basicaly the equation is to find out the length of a parabola lets say of a bridge or something.
Re: Proof of equation
Newton 20 Nov 2015, 08:12
Hello Hasham
Ah, I see. "Length of parabola" possibly means the curve length, for which you need integration, not differentiation. See the last example on this page:
5. Integration: Other Trigonometric Forms
Is that what you mean?
I think it best if you draw a diagram then we'll both be talking about the same thing.
Another point: "y= length of parabola of a structure" is not quite correct here - actually, `y` will be the height of the parabola `x` units from the origin.
X
Hello Hasham
Ah, I see. "Length of parabola" possibly means the curve length, for which you need integration, not differentiation. See the last example on this page:
<a href="/methods-integration/5-integration-other-trigonometric-forms.php">5. Integration: Other Trigonometric Forms</a>
Is that what you mean?
I think it best if you draw a diagram then we'll both be talking about the same thing.
Another point: "y= length of parabola of a structure" is not quite correct here - actually, `y` will be the height of the parabola `x` units from the origin.
Re: Proof of equation
Hasham 21 Nov 2015, 08:02
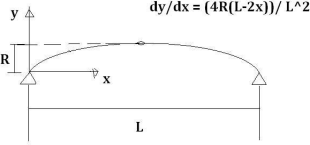
hi,
now i attached the fig. i have to explain the things as posible to me.
w8ing for the solution.
X
hi,
now i attached the fig. i have to explain the things as posible to me.
w8ing for the solution.
<img src="/forum/uploads/parabola310.png" width="310" height"145" alt="parabola" />
Re: Proof of equation
Newton 22 Nov 2015, 00:40
Hmmm - your diagram is fine (it represents the parabola you were talking about at the beginning), but you now have `dy/dx` at the beginning, which is a bit confused.
To find the arc length of a parabola, you need integration, not differentiation.
So let's clarify - is your question asking for the arc length of this parabola?
X
Hmmm - your diagram is fine (it represents the parabola you were talking about at the beginning), but you now have `dy/dx` at the beginning, which is a bit confused.
To find the arc length of a parabola, you need integration, not differentiation.
So let's clarify - is your question asking for the arc length of this parabola?
Re: Proof of equation
Hasham 23 Nov 2015, 03:20
Yes, I need to find the length of the parabola.
X
Yes, I need to find the length of the parabola.
Re: Proof of equation
Murray 24 Nov 2015, 00:30
OK, please post your actual question (which is not asking for a proof, nor for differentiating the expression) in the Applications of Integration forum.
X
OK, please post your actual question (which is not asking for a proof, nor for differentiating the expression) in the <a href="/forum/applications-integration-30/">Applications of Integration</a> forum.
Related Applications of Differentiation questions
- curve sketching [Solved!]
Wrote you earlier today. Confusion might come from Example 4. Three lines before... phinah 02 Nov 2017, 05:09
- Concavity [Solved!]
In curve sketching with differentiation, the general curves section, there are no points of inflection... phinah 02 Nov 2017, 03:30
- Practical application - normal to a curve? [Solved!]
Hi there. First off, I just wanted to say a huge thank you for the... Daniel 10 Dec 2015, 09:40
- Rate of change: conical tank [Solved!]
Please help me solve a rate of change problem about a conical tank wit vertex... Ana 25 Nov 2015, 09:46
Applications of Differentiation lessons on IntMath
top
