Differential Equations
Differential equations are a special type of integration problem.
Here is a simple differential equation of the type that we met earlier in the Integration chapter:
`(dy)/(dx)=x^2-3`
We didn't call it a differential equation before, but it is one. We'll see several different types of differential equations in this chapter.
Why are we doing this?
There are many applications of differential equations, including:
In this Differential Equations Chapter
In this chapter we will learn about:
Definition and Solution of DEs
- Predicting AIDS - a DEs example
- 1. Solving Differential Equations, write equations in differential form, solve simple differential equations and recognise different types of differential equations
- 2. Separation of Variables - a method of solving differential equations
- 3. Integrable Combinations - a method of solving differential equations
- 4. Linear DEs of Order 1 - and how to solve them
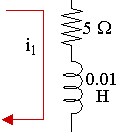
Applications - Electronics
- 5. Application: RL Circuits - containing a resistor and inductor
- 6. Application: RC Circuits - containing a resistor and capacitor
Second Order Differential Equations
- 7. Second Order DEs - Homogeneous - definition and method of solution
- 8. Second Order DEs - Damping - RLC - in a circuit with resistor, inductor and capacitor
- 9. Second Order DEs - Forced Response - constant and non-constant driving forces
- 10. Second Order DEs - Solve Using SNB - solving DEs using a computer algebra system
Before we see how to solve differential equations, let's see an example of them in action in the AIDS example.