12. Runge-Kutta (RK4) numerical solution for Differential Equations
In the last section, Euler's Method gave us one possible approach for solving differential equations numerically.
The problem with Euler's Method is that you have to use a small interval size to get a reasonably accurate result. That is, it's not very efficient.
The Runge-Kutta Method produces a better result in fewer steps.
Runge-Kutta Method Order 4 Formula
Applications of RK4
Mechanics
- Springs and dampeners on cars (This spring applet uses RK4.)
Biology
- Predator-prey models
- Fisheries collapses
- Drug delivery
- Epidemic prediction
Physics
- Climate change models
- Ozone protection
Aviation
- On-board computers
- Aerodynamics
`y(x+h)` `=y(x)+` `1/6(F_1+2F_2+2F_3+F_4)`
where
`F_1=hf(x,y)`
`F_2=hf(x+h/2,y+F_1/2)`
`F_3=hf(x+h/2,y+F_2/2)`
`F_4=hf(x+h,y+F_3)`
Where does this formula come from?
Here's a brief background to the formula.
Formula derivation
We learned earlier that Taylor's Series gives us a reasonably good approximation to a function, especially if we are near enough to some known starting point, and we take enough terms.
However, one of the drawbacks with Taylor's method is that you need to differentiate your function once for each new term you want to calculate. This can be troublesome for complicated functions, and doesn't work well in computerised modelling.
Carl Runge (pronounced "roonga") and Wilhelm Kutta (pronounced "koota") aimed to provide a method of approximating a function without having to differentiate the original equation.
Their approach was to simulate as many steps of the Taylor's Series method but using evaluation of the original function only.
Runge-Kutta Method of Order 2
We begin with two function evaluations of the form:
`F_1=hf(x,y)`
`F_2=hf(x+alpha h,y+beta F_1)`
The `alpha` and `beta` are unknown quantities. The idea was to take a linear combination of the `F_1` and `F_2` terms to obtain an approximation for the `y` value at `x = x_0+h`, and to find appropriate values of `alpha` and `beta`.
By comparing the values obtains using Taylor's Series method and the above terms (I will spare you the details here), they obtained the following, which is Runge-Kutta Method of Order 2:
`y(x+h)=y(x)+1/2(F_1+F_2)`
where
`F_1=hf(x,y)`
`F_2=hf(x+h,y+F_1)`
Runge-Kutta Method of Order 3
As usual in this work, the more terms we take, the better the solution. In practice, the Order 2 solution is rarely used because it is not very accurate.
A better result is given by the Order 3 method:
`y(x+h)=` `y(x)+1/9(2F_1+3F_2+4F_3)`
where
`F_1=hf(x,y)`
`F_2=hf(x+h/2,y+F_1/2)`
`F_3=hf(x+(3h)/4,y+(3F_2)/4)`
This was obtained in a similar way to the earlier formula, by comparing Taylor's Series results.
The most commonly used Runge-Kutta formula in use is the Order 4 formula (RK4), as it gives the best trade-off between computational requirements and accuracy.
Let's look at an example to see how it works.
Example
Use Runge-Kutta Method of Order 4 to solve the following, using a step size of `h=0.1` for `0lexle1`.
`dy/dx=(5x^2-y)/e^(x+y)`
`y(0) = 1`
Step 1
Note: The following looks tedious, and it is. We'll use a computer (not calculator) to do most of the work for us. The following is here so you can see how the formula is applied.
We start with `x=0` and `y=1`. We'll find the `F` values first:
`F_1=hf(x,y)` ` = 0.1(5(0)^2-1)/e^(0+1)` ` = -0.03678794411`
For `F_2`, we need to know:
`x+h/2 = 0+0.1/2 = 0.05`, and
`y+F_1/2` ` = 1 + (-0.03678794411)/2` ` = 0.98160602794`
We substitute these into the `F_2` expression:
`F_2=hf(x+h/2,y+F_1/2)` ` = 0.1((5(0.05)^2-0.98160602794)/e^(0.05+0.98160602794))` `=-0.03454223937`
For `F_3`, we need to know:
`y+F_2/2` ` = 1 + (-0.03454223937)/2` ` = 0.98272888031`
So
`F_3=hf(x+h/2,y+F_2/2)` ` = 0.1((5(0.05)^2-0.98272888031)/e^(0.05+0.98272888031))` `=-0.03454345267`
For `F_4`, we need to know:
`y+F_3` ` = 1 -0.03454345267` ` = 0.96545654732`
So
`F_4=hf(x+h,y+F_3)` ` = 0.1((5(0.1)^2-0.96545654732)/e^(0.1+0.96545654732))` `= -0.03154393258`
Step 2
Next, we take those 4 values and substitute them into the Runge-Kutta RK4 formula:
`y(x+h)` `=y(x)+1/6(F_1+2F_2+2F_3+F_4)`
`=1+1/6( -0.03678794411` ` -\ 2xx0.03454223937` `-\ 2 xx0.03454345267` `{:-\ 0.03154393258)`
`=0.9655827899`
Using this new `y`-value, we would start again, finding the new `F_1`, `F_2`, `F_3` and `F_4`, and substitute into the Runge-Kutta formula.
We continue with this process, and construct the following table of Runge-Kutta values. (I used a spreadsheet to obtain the table. Using calculator is very tedious, and error-prone.)
| `x` | `y` | `F_1 = h dy/dx` | `x+h/2` | `y+F_1/2` | `F_2` | `y+F_2/2` | `F_3` | `x+h` | `y+F_3` | `F_4` |
| 0 | 1 | −0.0367879441 | 0.05 | 0.9816060279 | −0.0345422394 | 0.9827288803 | −0.0345434527 | 0.1 | 0.9654565473 | −0.0315439326 |
| 0.1 | 0.9655827899 | −0.0315443 | 0.15 | 0.9498106398 | −0.0278769283 | 0.9516443257 | −0.0278867954 | 0.2 | 0.9376959945 | −0.023647342 |
| 0.2 | 0.937796275 | −0.023648185 | 0.25 | 0.9259721824 | −0.0189267761 | 0.9283328869 | −0.0189548088 | 0.3 | 0.9188414662 | −0.0138576597 |
| 0.3 | 0.9189181059 | −0.0138588628 | 0.35 | 0.9119886745 | −0.0084782396 | 0.9146789861 | −0.0085314167 | 0.4 | 0.9103866892 | −0.0029773028 |
| 0.4 | 0.9104421929 | −0.0029786344 | 0.45 | 0.9089528756 | 0.0026604329 | 0.9117724093 | 0.002580704 | 0.5 | 0.9130228969 | 0.0082022376 |
| 0.5 | 0.913059839 | 0.0082010354 | 0.55 | 0.9171603567 | 0.013727301 | 0.9199234895 | 0.0136258867 | 0.6 | 0.9266857257 | 0.018973147 |
| 0.6 | 0.9267065986 | 0.0189722976 | 0.65 | 0.9361927474 | 0.0240794197 | 0.9387463085 | 0.0239658709 | 0.7 | 0.9506724696 | 0.0287752146 |
| 0.7 | 0.9506796142 | 0.0287748718 | 0.75 | 0.9650670501 | 0.0332448616 | 0.967302045 | 0.0331305132 | 0.8 | 0.9838101274 | 0.0372312889 |
| 0.8 | 0.9838057659 | 0.0372315245 | 0.85 | 1.0024215282 | 0.0409408747 | 1.0042762033 | 0.0408359751 | 0.9 | 1.024641741 | 0.0441484563 |
| 0.9 | 1.024628046 | 0.0441492608 | 0.95 | 1.0467026764 | 0.0470593807 | 1.0481577363 | 0.0469712279 | 1 | 1.0715992739 | 0.0494916177 |
| 1 | 1.0715783953 |
I haven't included any values after `y` in the bottom row as we won't be using them.
Here is the graph of the solutions we found, from `x=0` to `x=1`.
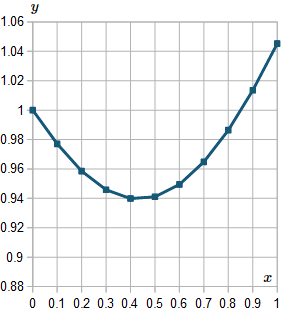
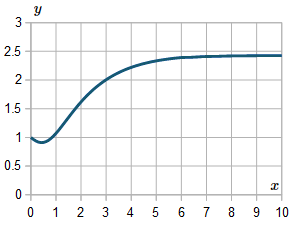
For interest, I extended the result up to `x=10`, and here is the resulting graph:
Exercise
Solve the following using RK4 (Runge-Kutta Method of Order 4) for `0 le x le 2`. Use a step size of `h=0.2`:
`dy/dx=(x+y)sin xy`
`y(0) = 5`
Answer
Step 1
We have `x_0=0` and `y_0=5`.
`F_1=hf(x,y)` ` = 0.2((0+5)sin (0)(5))` ` = 0`
For `F_2`, we need to know:
`x+h/2 = 0+0.2/2 = 0.1`, and
`y+F_1/2 = 5+0/2=5 `
We substitute these into the `F_2` expression:
`F_2=hf(x+h/2,y+F_1/2)` ` = 0.2((0.1+5)sin (0.1)(5))` `=0.48901404937`
For `F_3`, we need to know:
`y+F_2/2` ` = 5+0.48901404937/2` `=5.24450702469`
So
`F_3=hf(x+h/2,y+F_2/2) `
`= 0.2((0.1+5.24450702469)` `{:xxsin (0.1)(5.24450702469))`
`=0.53523913352`
For `F_4`, we need to know:
`y+F_3` ` = 5+0.53523913352` ` = 5.53523913352 `
So
`F_4=hf(x+h,y+F_3)`
` = 0.2((0.2+5.53523913352)` `{:xxsin (0.2)(5.53523913352))`
`= 1.02589900571`
Step 2
Next, we take those 4 values and substitute them into the Runge-Kutta RK4 formula:
`y(x+h)=y(x)+1/6(F_1+2F_2+2F_3+F_4)`
`=5+1/6(0+ ` `2xx0.48901404937+ ` `2xx0.53523913352 ` `{:+ 1.02589900571)`
`=5.5124008953`
As before, we need to take this `y_1` value and use the new `x_1=0.2` value to find the next value, `y_2`, and so on up to `x=2`.
Following is the table of resulting values.
Here's the table of values we get.
View table
| `x` | `y` | `F_1 = h dy/dx` | `x+h/2` | `y+F_1/2` | `F_2` | `y+F_2/2` | `F_3` | `x+h` | `y+F_3` | `F_4` |
| 0 | 5 | 0 | 0.1 | 5 | 0.4890140494 | 5.2445070247 | 0.5352391335 | 0.2 | 5.5352391335 | 1.0258990057 |
| 0.2 | 5.5124008953 | 1.0194689011 | 0.3 | 6.0221353458 | 1.229424454 | 6.1271131223 | 1.2397613573 | 0.4 | 6.7521622525 | 0.6102193187 |
| 0.4 | 6.6070775356 | 0.670350862 | 0.5 | 6.9422529666 | -0.4816655538 | 6.3662447588 | -0.0570142602 | 0.6 | 6.5500632755 | -1.0142481364 |
| 0.6 | 6.3702013853 | -0.8771352065 | 0.7 | 5.931633782 | -1.1235642458 | 5.8084192624 | -1.0390037691 | 0.8 | 5.3311976162 | -1.1055304726 |
| 0.8 | 5.3189011004 | -1.0980514561 | 0.9 | 4.7698753724 | -1.0356506358 | 4.8010757825 | -1.0539783626 | 1 | 4.2649227378 | -0.9493143311 |
| 1 | 4.2811304698 | -0.9595184486 | 1.1 | 3.8013712455 | -0.8453508288 | 3.8584550553 | -0.8850171765 | 1.2 | 3.3961132933 | -0.7389191476 |
| 1.2 | 3.421268202 | -0.7592177155 | 1.3 | 3.0416593442 | -0.6304549629 | 3.1060407205 | -0.6882207337 | 1.4 | 2.7330474682 | -0.5227646767 |
| 1.4 | 2.7680459044 | -0.5581856458 | 1.5 | 2.4889530815 | -0.4450766109 | 2.5455075989 | -0.5066587622 | 1.6 | 2.2613871422 | -0.354308929 |
| 1.6 | 2.2987183509 | -0.3984550218 | 1.7 | 2.09949084 | -0.3150804545 | 2.1411781236 | -0.3672394563 | 1.8 | 1.9314788946 | -0.2454079264 |
| 1.8 | 1.9639678892 | -0.2886730166 | 1.9 | 1.8196313809 | -0.230980612 | 1.8484775833 | -0.2714612259 | 2 | 1.6925066634 | -0.1779964411 |
| 2 | 1.7187090337 |
Once again, I haven't included any values after `y` in the bottom row as they are not required.
Here is the graph of the solutions we found, from `x=0` to `x=2`.
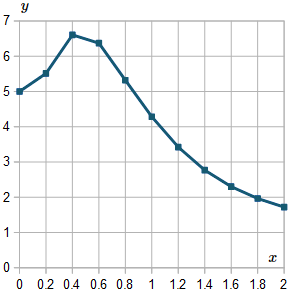
For interest, I extended the result up to `x=6`, and here is the resulting graph:
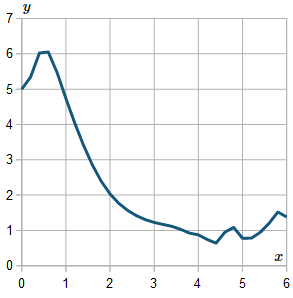
We observe the graph is not very smooth. If we use a smaller `h` value, the curve will generally be smoother.
In fact, this curve is asymptotic to the `x`-axis (it smoothly gets closer to the axis as `x` gets larger). The above graph shows what happens when our intervals are too coarse. (Those wiggles after around `x>4.5` should not be there.)
Here is the solution graph again, but this time I've used `h=0.1`. It's better, but still has a "wiggle" near `x=5` that should not be there.
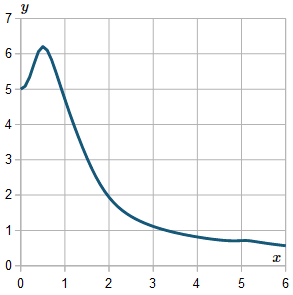
If I took even smaller values of `h`, I'd get a smoother curve. However, that's only up to a point, because rounding errors become significant eventually. Also, computing time goes up for little added benefit.
Improvements to Runge-Kutta
As you can see from the above example, there are points in the curve where the `y` values change relatively quickly (between `0` and `1`) and other places where the curve is more nearly linear (from `1` to `2`). Also, we have strange behavior near `x=5`.
In practice, when writing a computer program to perform Runge-Kutta, we allow for variable `h` values - quite small when the curve is changing quickly, and larger `h` values when the curve is relatively smooth.
Mathematics computer algebra systems (like Mathcad, Mathematica and Maple) include routines that calculate RK4 for us, so we just need to provide the function and the interval of interest.
Caution
Always be wary of your answers! Numerical solutions are only ever approximations, and under certain conditions, you can get chaotic results.
Problem Solver
Need help solving a different Calculus problem? Try the Problem Solver.
Disclaimer: IntMath.com does not guarantee the accuracy of results. Problem Solver provided by Mathway.