11. Euler's Method - a numerical solution for Differential Equations
Why numerical solutions?
For many of the differential equations we need to solve in the real world, there is no "nice" algebraic solution. That is, we can't solve it using the techniques we have met in this chapter (separation of variables, integrable combinations, or using an integrating factor), or other similar means.
As a result, we need to resort to using numerical methods for solving such DEs. The concept is similar to the numerical approaches we saw in an earlier integration chapter (Trapezoidal Rule, Simpson's Rule and Riemann Sums).
Even if we can solve some differential equations algebraically, the solutions may be quite complicated and so are not very useful. In such cases, a numerical approach gives us a good approximate solution.
The General Initial Value Problem
We are trying to solve problems that are presented in the following way:
`dy/dx=f(x,y)`; and
`y(a)` (the inital value) is known,
where `f(x,y)` is some function of the variables `x`, and `y` that are involved in the problem.
Examples of Initial Value Problems
(a) `dy/dx=6-2y/x`
`y(3)=1`
(b) `dy/dx=(y ln y)/x`
`y(2)=e`
(c) `dy/dx=(50x^2-10y)/3`
`y(0)=0`
Note that the right hand side is a function of `x` and `y` in each case.
Let's now see how to solve such problems using a numerical approach.
Euler's Method
Euler's Method assumes our solution is written in the form of a Taylor's Series.
That is, we'll have a function of the form:
`y(x+h)` `~~y(x)+h y'(x)+(h^2y''(x))/(2!)` `+(h^3y'''(x))/(3!)` `+(h^4y^("iv")(x))/(4!)` `+...`
This gives us a reasonably good approximation if we take plenty of terms, and if the value of `h` is reasonably small.
For Euler's Method, we just take the first 2 terms only.
`y(x+h)` `~~y(x)+h y'(x)`
The last term is just `h` times our `dy/dx` expression, so we can write Euler's Method as follows:
`y(x+h)` `~~y(x)+h f(x,y)`
How do we use this formula?
We start with some known value for `y`, which we could call `y_0`. It has this value when `x=x_0`. (We make use of the initial value `(x_0,y_0)`.)
The result of using this formula is the value for `y`, one `h` step to the right of the current value. Let's call it `y_1`. So we have:
`y_1` `~~y_0+h f(x_0,y_0)`
where
`y_1` is the next estimated solution value;
`y_0` is the current value;
`h` is the interval between steps; and
`f(x_0,y_0)` is the value of the derivative at the starting point, `(x_0,y_0)`.
Next value: To get the next value `y_2`, we would use the value we just found for `y_1` as follows:
`y_2` `~~y_1+h f(x_1,y_1)`
where
`y_2` is the next estimated solution value;
`y_1` is the current value;
`h` is the interval between steps;
`x_1 = x_0+h`; and
`f(x_1,y_1)` is the value of the derivative at the current `(x_1,y_1)` point.
We continue this process for as many steps as required.
What's going on?
The right hand side of the formula above means, "start at the known `y` value, then move one step `h` units to the right in the direction of the slope at that point, which is `dy/dx = f(x,y)`. We will arrive at a good approximation to the curve's y-value at that new point."
We'll do this for each of the sub-points, `h` apart, from some starting value `x=a` to some finishing value, `x=b`, as shown in the graph below.
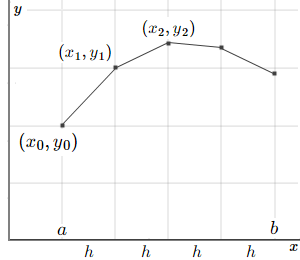
Let's see how it works with an example.
Example: Euler's Method
Let's solve example (b) from above. We had the initial value problem:
`dy/dx=(y ln y)/x`
`y(2)=e`
Step 1
We'll start at the point `(x_0,y_0)=(2,e)` and use step size of `h=0.1` and proceed for 10 steps. That is, we'll approximate the solution from `t=2` to `t=3` for our differential equation. We'll finish with a set of points that represent the solution, numerically.
We already know the first value, when `x_0=2`, which is `y_0=e` (the initial value).
We now calculate the value of the derivative at this initial point. (This tells us the direction to move.)
`dy/dx = f(2,e)` `=(e ln e)/2` ` = e/2~~1.3591409`
This means the slope of the line from `t=2` to `t=2.1` is approximately `1.3591409`.
Step 2
Now, for the second step, (since `h=0.1`, the next point is `x+h=2+0.1=2.1`), we substitute what we know into Euler's Method formula, and we have:
`y(x+h)` `~~y(x)+h f(x,y)`
`y_1 = y(2.1)` ` ~~ e + 0.1(e/2)` ` = 2.8541959`
This means the approximate value of the solution when `x=2.1` is `2.8540959`.
Let's see what we've done on a graph.
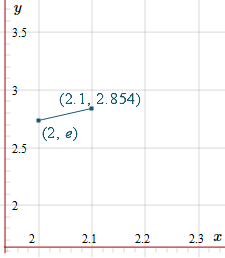
We'll need the new slope at this point, so we'll know where to head next.
`dy/dx = f(2.1,2.8541959)` `=(2.8541959 ln 2.8541959)/2.1` ` = 1.4254536`
This means the slope of the approximation line from `x=2.1` to `x=2.2` is `1.4254536`. So it's a little bit steeper than the first slope we found.
Step 3
Now we are trying to find the solution value when `x=2.2`. We substitute our known values:
`y(x+h)` `~~y(x)+h f(x,y)`
`y(2.2) ~~` ` 2.8540959 + 0.1(1.4254536)` ` = 2.99664126`
With this new value, our graph is now:
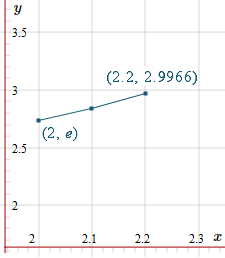
We'll need the new slope at this point, so we'll know where to head next.
`f(2.2,2.99664126)` `=(2.99664126 ln 2.99664126)/2.2` ` = 1.49490457`
This means the slope of the approximation line from `x=2.2` to `x=2.3` is `1.49490456`. So it's a little more steep than the first 2 slopes we found.
Step 4
Now we are trying to find the solution value when `x=2.3`. We substitute our known values:
`y(x+h)` `~~y(x)+h f(x,y)`
`y(2.3) ~~` ` 2.99664126 + 0.1(1.49490456)` ` = 3.1461317`
With this new value, our graph is now:
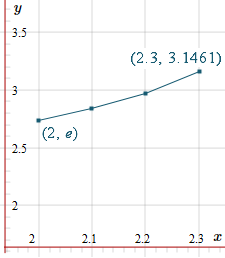
Subsequent Steps
We present all the values up to `x=3` in the following table.
Of course, most of the time we'll use computers to find these approximations. I used a spreadsheet to obtain the following values. Don't use your calculator for these problems - it's very tedious and prone to error. You could use an online calculator, or Google search.
| `x` | `y` | `dy/dx` |
| 2.0 | e = 2.7182818285 | (e ln e)/2 = 1.3591409142 |
| 2.1 | e+0.1(e/2) = 2.8541959199 | (2.8541959199 ln 2.8541959199)/2 = 1.4254536226 |
| 2.2 | 2.9967412821 | 1.4949999323 |
| 2.3 | 3.1462412754 | 1.5679341197 |
| 2.4 | 3.3030346873 | 1.6444180873 |
| 2.5 | 3.4674764961 | 1.7246216904 |
| 2.6 | 3.6399386651 | 1.8087230858 |
| 2.7 | 3.8208109737 | 1.8969091045 |
| 2.8 | 4.0105018841 | 1.9893756448 |
| 2.9 | 4.2094394486 | 2.08632809 |
| 3.0 | 4.4180722576 |
(There's no final `dy/dx` value because we don't need it. We've found all the required `y` values.)
Here is the graph of our estimated solution values from `x=2` to `x=3`.
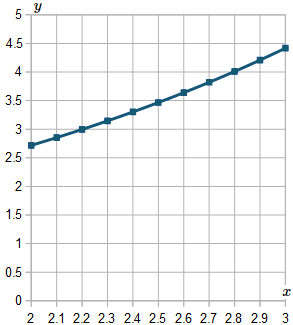
How good is it?
This particular question actually is easy to solve algebraically, and we did it back in the Separation of Variables section. (It was Example 7.)
Our solution was `y = e^(x"/"2)`. In the next graph, we see the estimated values we got using Euler's Method (the dark-colored curve) and the graph of the real solution `y = e^(x"/"2)` in magenta (pinkish). We can see they are very close.
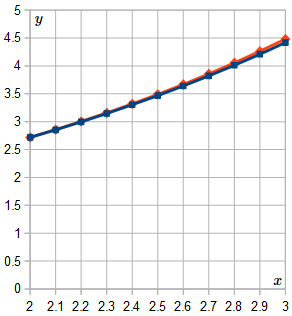
In this case, the solution graph is only slightly curved, so it's "easy" for Euler's Method to produce a fairly close result.
In fact, at `x=3` the actual solution is `y=4.4816890703`, and we obtained the approximation `y=4.4180722576`, so the error is only:
`(4.4816890703 - 4.4180722576)/4.4816890703` ` = 1.42%`.
Exercise
The following question cannot be solved using the algebraic techniques we learned earlier in this chapter, so the only way to solve it is numerically.
Solve using Euler's Method:
`dy/dx=sin(x+y)-e^x`
`y(0) = 4`
Use `h=0.1`
Answer
Step 1
We start at the initial value `(0,4)` and calculate the value of the derivative at this point. We have:
`dy/dx=sin(x+y)-e^x`
`=sin(0+4)-e^0`
`=-1.75680249531`
We substitute our starting point and the derivative we just found to obtain the next point along.
`y(x+h)~~y(x)+hf(x,y)`
`y(0.1)~~4+0.1(-1.75680249531)`
`~~3.82431975047`
Step 2
Now we need to calculate the value of the derivative at this new point `(0.1,3.82431975047)`. We have:
`dy/dx=sin(x+y)-e^x`
`=sin(0.1+3.82431975047)` `-e^0.1`
`=-1.8103864498`
Once again, we substitute our current point and the derivative we just found to obtain the next point along.
`y(x+h)~~y(x)+hf(x,y)`
`y(0.2)~~3.82431975047+` `0.1(-1.8103864498)`
`~~3.64328110549`
We proceed for the required number of steps and obtain these values:
| `x` | `y` | `dy/dx` |
| 0 | 4 | -1.7568024953 |
| 0.1 | 3.8243197505 | -1.8103864498 |
| 0.2 | 3.6432811055 | -1.8669109257 |
| 0.3 | 3.4565900129 | -1.926815173 |
| 0.4 | 3.2639084956 | -1.9907132334 |
| 0.5 | 3.0648371723 | -2.0594421065 |
| 0.6 | 2.8588929616 | -2.1341215746 |
| 0.7 | 2.6454808042 | -2.2162311734 |
| 0.8 | 2.4238576868 | -2.3077132045 |
| 0.9 | 2.1930863664 | -2.4111158431 |
| 1 | 1.9519747821 |
Here's the graph of this solution.
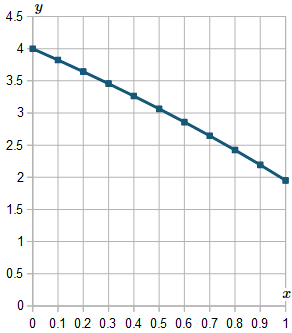
In the next section, we see a more sophisticated numerical solution method for differential equations, called the Runge-Kutta Method.
Problem Solver
Need help solving a different Calculus problem? Try the Problem Solver.
Disclaimer: IntMath.com does not guarantee the accuracy of results. Problem Solver provided by Mathway.
