9. Mutually Exclusive Events
Two or more events are said to be mutually exclusive if the occurrence of any one of them means the others will not occur (That is, we cannot have 2 or more such events occurring at the same time).
For example, if we throw a 6-sided die, the events "4" and "5" are mutually exclusive. We cannot get both 4 and 5 at the same time when we throw one die.
If E1 and E2 are mutually exclusive events, then E1 and E2 will not happen together. So the probabality of the 2 events will be zero:
P(E1 and E2) = 0.
Now, suppose "E1 or E2" denotes the event that "either E1 or E2 both occur", then
(a) If E1 and E2 are not mutually exclusive events:
P(E1 or E2) = P(E1) + P(E2) − P(E1 and E2)
We can also write:
P(E1 ∪ E2) = P(E1) + P(E2) − P(E1 ∩ E2)
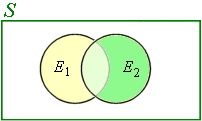
A diagram for this situation is as follows. We see that there is some overlap between the events E1 and E2. The probability of that overlap portion is P(E1 ∩ E2).
An example for non-mutually exclusive events could be:
E1 = students in the swimming team
E2 = students in the debating team
In this case, the yellow area represents students in the swimming team only, and the darker green area represents students in the debating team only. The light green overlap area represents the students in both the swimming team and the debating team.
(b) If E1 and E2 are mutually exclusive events:
P(E1 or E2) = P(E1) + P(E2)
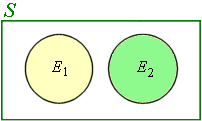
Our diagram for mutually exclusive events shows that there is no overlap:
An example of mutually exclusive events could be:
E1 = male students
E2 = female students
There is no overlap. [Of course, gender is not a simple issue as in fact, some overlap does occur. Don't read too much into it — this is just an example.]
In this case, the intersection E1 ∩ E2 is empty, leading to the conclusion:
P(E1 ∩ E2) = 0
This explains why, for the mutually exclusive case,
P(E1 or E2) = P(E1) + P(E2)
Example 1
It is known that the probability of obtaining zero defectives in a sample of `40` items is `0.34` whilst the probability of obtaining `1` defective item in the sample is `0.46`. What is the probability of
(a) obtaining not more than `1` defective item in a sample?
(b) obtaining more than `1` defective items in a sample?
Answer
"Obtaining not more than one" means we choose either `0` or `1` defective.
Let event E1 be "obtaining zero defectives" and E2 be "obtaining `1` defective item".
(a) Events E1 and E2 are mutually exclusive, so
P(E1 or E2) = P(E1) + P(E2) = 0.34 + 0.46 = 0.8
(b) `P("more than 1") = 1 − 0.8 = 0.2`
Example 2
The probability that a student passes Mathematics is `2/3` and the probability that he passes English is `4/9`. If the probability that he will pass at least one subject is `4/5`, what is the probability that he will pass both subjects?
(We assume it is based on probability only.)
Answer
It is possible for a student to either:
- Pass math only
- Pass English only
- Pass both math and English
So we conclude that these are not mutually exclusive events. We have:
P(E1 or E2) = P(E1) + P(E2) − P(E1 and E2)
Substituting:
`4/5=2/3+4/9-P(E_1 "and" E_2)`
So
`P(E_1 "and" E_2)` ` = 2/3 + 4/9-4/5` `=14/45`
Assorted Exercises
Exercise 1
A box contains `100` items of which `4` are defective. Two items are chosen at random from the box. What is the probability of selecting
(a) `2` defectives if the first item is not replaced;
(b) `2` defectives if the first item is put back before choosing the second item;
(c) `1` defective and 1 non-defective if the first item is not replaced?
Answer
(a) On the first draw, there are `4` defectives in the box out of the `100` total items.
If we have already chosen one of the defectives on the first draw, then on the second draw, there will be `3` defectives left out of the `99` items in the box. The required probability is:
`4/100 times 3/99 = 1/825 = 1.2121 times 10^-3`
(b) Both the first draw and the second draw have the same probability of getting a defective, i.e. `4` in `100`. The required probability is:
`4/100 times 4/100 = 1/625 = 0.0016`
(c) We can either:
- Get a defective on the first draw (`4` chances in `100`) then a non-defective on the second (`96` non-defectives out of `99` left in the box); OR
- Get a non-defective first (`96` chances in `100`) then a defective (`4` in the remaining `99`).
So the probability is
`(4/100) × (96/99) + (96/100) × (4/99),`
which can also be written as:
`"Prob" = 4/100 times 96/99 times 2`
` = 64/825`
`=7.7576times10^-2`
Note: In probability, the word "OR" in the question usually means we need to add the probabilities.
Exercise 2
Five small radios are packed in identical, unmarked individual sealed boxes. Three boxes are on table X and contain 2 radios made by firm A and one by firm B. Two boxes are on table Y and contain one radio made by firm A and one by firm B. If someone moves a box from table X to table Y and you randomly select a box from table Y, what is the probability that you will select a radio made by firm B?
Answer
At first:
Table `X`: `A AB`
Table `Y`: `AB`
Let
P(AX) = probability of selecting `A` from `X`
P(BX) = probability of selecting `B` from `X`
P(BY) = probability of selecting `B` from `Y`
`P(B_Y) = P(A_X) times P(B_Y|A_X) +` ` P(B_X) times P(B_Y|B_X)`
`=2/3 times 1/3 + 1/3 times 2/3`
`=4/9`
Exercise 3
If the independent probabilities that three people A, B and C will be alive in `30` years time are `0.4, 0.3, 0.2` respectively, calculate the probability that in `30` years' time,
(a) all will be alive
(b) none will be alive
(c) only one will be alive
(d) at least one will be alive
Answer
(a) P = P(A) × P(B) × P(C) = 0.4 × 0.3 × 0.2 = 0.024
(b) We use the notation `P(barA)` to mean "the probability that A will not occur". So:
`P=P(barA)xxP(barB)xxP(barC)`
`=0.6xx0.7xx0.8`
`=0.336`
(c) `P=P(A\ "only alive") ` `+ P(B\ "only alive") ` `+ P(C\ "only alive")`
`=[P(A) times P(barB) times P(barC)]` `+[P(barA) times P(B) times P(barC)] ` `+ [P(barA) times P(barB) times P(C)]`
`=0.4 times 0.7times0.8` `+0.6times0.3times0.8` `+0.6times0.7times0.2`
`=0.452`
(d) `P=1-` `{P(barA)xxP(barB)xxP(barC) } ` `=1-0.336` `=0.664`