10. Bayes' Theorem

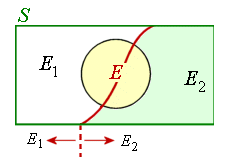
Let E₁ and E₂ be two mutually exclusive events forming a partition of the sample space S and let E be any event of the sample space such that P(E) ≠ 0.

Example 1

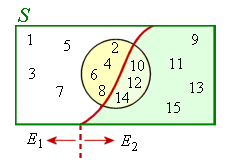
The sample space S is described as "the integers `1` to `15`" and is partitioned into:

E₁ = "the integers `1` to `8`" and

E₂ = "the integers `9` to `15`".

If E is the event "even number" then we have the following:

[Recall from Conditional Probability that the notation P(E₁ | E) means "the probability of the event E₁ given that E has already occurred".]

Statement of Bayes' Theorem

The probabilities for the situation described above is given by Bayes' Theorem, which can be calculated in two ways:

Method 1

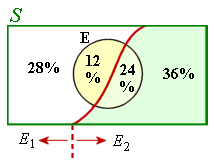
So for our example above, checking both items of this equation:

Method 2

We get the same result using the second form:

Extending Bayes' Theorem for Mutually Exclusive Events

Bayes' Theorem can be extended as follows:

If E₁, E₂, ... , E_k are mutually exclusive events forming partitions of the sample space S and if E is any event of S such that P(E) ≠ 0, then

`P(E_i|E)=(P(E_i nnnE))/(P(E_1nnnE)+P(E_2nnnE)+...+P(E_knnnE))`

Example 2

Of all the smokers in a particular district, `40%` prefer brand `A` and `60%` prefer brand `B`. Of those smokers who prefer brand `A`, `30%` are females, and of those who prefer brand `B`, `40%` are female. What is the probability that a randomly selected smoker prefers brand `A`, given that the person selected is a female?

Answer

Example 3

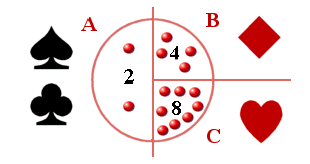
There are 3 urns `A`, `B` and `C` each containing a total of `10` marbles of which `2`, `4` and `8` respectively are red. A pack of cards is cut and a marble is taken from one of the urns depending on the suit shown - a black suit indicating urn `A`, a diamond urn `B`, and a heart urn `C`. What is the probability a red marble is drawn?

If somebody secretly cut the cards and drew out a marble and then announced to us a red marble had in fact been drawn, could we compute the probability of the cut being, say, a heart (or more generally, can we compute the probability of a specified prior event given that the subsequent event did occur)?

Answer

Further explanation of Bayes' Theorem

Here's 2 video explanations of Bayes' Theorem:

Friday math movie – NUMB3RS and Bayes’ Theorem