3. Division of Algebraic Expressions
Later, on this page
Our first examples of division of algebraic expressions involve simplifying and canceling.
Example 1
Simplify `(3ab(4a^2b^5))/(8a^2b^3)`
Answer
First, we multiply out the top line:
`(12a^3b^6)/(8a^2b^3)`
When we write it out in full, this means
`(12 xx aaa xx b b b b b b)/(8 xx aa xx b b b)`
Next, cancel the numbers top and bottom (we divide top and bottom by `4`), the "a" terms (we cancel `a^2=aa` from top and bottom) and the "b" terms (we cancel `b^3=b b b` from top and bottom) to give us the final answer:
`(3ab^3)/2`
Example 2
Simplify `(12m^2n^3)/((6m^4n^5)^2)`
Answer
We square the denominator (bottom) of the fraction:
`(12m^2n^3)/((6m^4n^5)^2)=(12m^2n^3)/(36m^8n^10)`
Next, we cancel out the numbers, and the "m" and "n" terms to give the final answer:
`1/(3m^6n^7)`
Example 3
Simplify `(6p^3q^2-10p^2q)/(4q)`
Answer
With this example, we'll break it into 2 fractions, both with denominator 4q to make it easier to see what to do.
`(6p^3q^2-10p^2q)/(4q)=(6p^3q^2)/(4q)-(10p^2q)/(4q)`
Next, we cancel the numbers and variables:
`(3p^3q)/2-(5p^2)/2`
Finally, we combine the fractions:
`(3p^3q-5p^2)/2`
After you have had some practice with these, you'll be able to do it without separating them into 2 fractions first.
Dividing by a Fraction
Recall the following when dividing algebraic expressions.
The reciprocal of a number x, is `1/x`.
For example, the reciprocal of 5 is `1/5` and the reciprocal of `1 2/3` is `3/5`.
To divide by a fraction, you multiply by the reciprocal of the fraction.
For example, `3/4 -: 7/x=3/4xxx/7=(3x)/28`
Example 4
Simplify
`(3+1/x)/(5/x+4)`
Answer
I'll show you how to do this two different ways. It is worth seeing both, because they are both useful. You can decide which is easier ;-)
Solution 1 - Multiplying by the Reciprocal
I take the top expression (numerator) and turn it into a single fraction with denominator x.
`3+1/x=(3x+1)/x`
We do likewise with the bottom expression (denominator):
`5/x+4=(5+4x)/x`
So the question has become:
`(3+1/x)/(5/x+4)=((3x+1)/x)/((5+4x)/x)`
We think of the right side as a division of the top by the bottom:
`(3x+1)/x-:(5+4x)/x`
To divide by a fraction, you multiply by the reciprocal:
`(3x+1)/(x)xxx/(5+4x)=(3x+1)/(5+4x)`
The x's cancelled out, and we have our final answer, which cannot be simplified any more.
Solution 2 - Multiplying Top and Bottom
I recognise that I have "/x" in both the numerator and denominator. So if I just multiply top and bottom by x, it will simplify everything by removing the fractions on top and bottom.
`(3+1/x)/(5/x+4)xxx/x`
I am really just multiplying by "1" and not changing the original value of the fraction - just changing its form.
So I multiply each element of the top by x and each element of the bottom by x and I get:
`(3+1/x)/(5/x+4)xxx/x=(3x+1)/(5+4x)`
I cannot simplify any further.
Long Division in Algebra
Before we do an example using algebra, let’s remember how to do long division with numbers first.
Example 5
Let’s do 23,576 divided by 13.
We can write this as a fraction:
`23576/13`
Now, to divide this, (assuming we do not have a calculator) we could proceed as follows.
23 divided by 13 = 1 with remainder 10.
We bring the 5 (the next number after 3) down.
Now we have
105 divided by 13 is 8 with remainder 1
We continue until we get to the last number, 6.
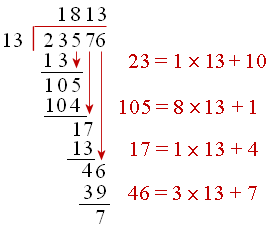
Our result means that the answer is 1,813 with remainder 7, or:
`23576/13=1813 7/13`
We use a similar technique for long division in algebra.
Example 6 - Algebraic Long Division
Simplify `(3x^2-11x-4)-:(x-4)`
Answer
We are dividing a polynomial of degree 2 by a polynomial of degree 1. This is algebraic long division.
Step 1: We look at the first term of (3x2 − 11x − 4) and the first term of (x − 4).
Divide as follows: 3x2 ÷ x = 3x
We write 3x at top of our long division and multiply (3x)(x − 4) = 3x2 − 12x to give the second row of our solution.
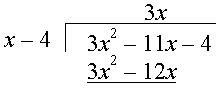
Step 2: Subtracting the second row from the first gives:
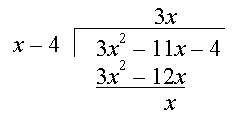
Be careful with
-11x − (-12x) = -11x + 12x = x
Step 3: Bring down the -4 from the first row:
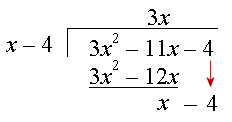
Step 4: Divide x (in the 3rd row) by x from the (x − 4) in the question. Our answer is 1 and we write "+ 1" at the top of our long division.
Next, multiply (1) by (x − 4) to get the 4th row.
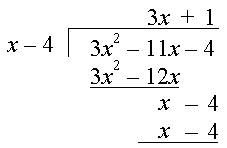
Step 5: Subtract the 4th row from the 3rd:
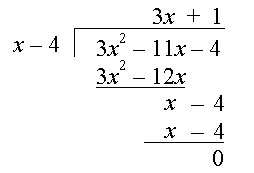
So (3x2 − 11x − 4) ÷ (x − 4) = 3x + 1
You can check your answer by multiplying (3x + 1) by (x − 4) and you'll get (3x2 − 11x − 4).
Example 7
Simplify `(6x^2+6+7x)/(2x+1)`
Answer
We can think of `(6x^2+6+7x)/(2x+1)` as (6x2 + 7x + 6) ÷ (2x + 1)
Once again we are dividing a polynomial of degree 2 by a polynomial of lower degree (1). This is algebraic long division.
Step 1: 6x2 ÷ 2x = 3x
So we write the following, using (3x)(2x + 1) = 6x2 + 3x for the second row:
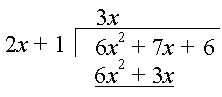
Step 2: We subtract 6x2 + 3x from the first row:
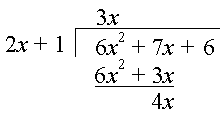
Step 3: Bring down the 6:
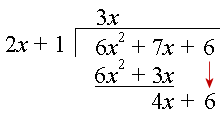
Step 4: Divide 4x by 2x. Our answer is 2 and we multiply 2(2x + 1) to get the 4th row.
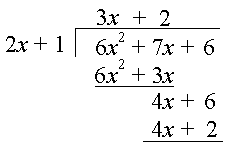
Step 5: Subtract, and we are left with 4.
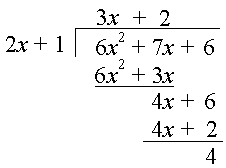
So the answer is:
`(6x^2+6+7x)/(2x+1)=3x+2+4/(2x+1)`
NOTE: Some people prefer to write the problem with all the x2's, x's and units in line, as follows:
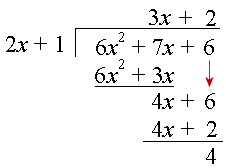
You can see how algebraic long division is used in a later section, Remainder and Factor Theorems.