6. Moments of Inertia by Integration
by M. Bourne
The moment of inertia is a measure of the resistance of a rotating body to a change in motion.
The moment of inertia of a particle of mass m rotating about a particular point is given by:
`"Moment of inertia" = md^2`
where d is the radius of rotation.
Inertia for a Collection of Particles
If a group of particles with masses m1, m2, m3, ... , mn is rotating around a point with distances d1, d2, d3, ... dn, (respectively) from the point, then the moment of inertia I is given by:
I = m1d12 + m2d22 + m3d32 +... + mndn2
If we wish to place all the masses at the one point (R units from the point of rotation) then
d1 = d2 = d3 = ... = dn = R and we can write:
I = (m1 + m2 + m3 ... + mn)R2
R is called the radius of gyration.
Example 1
Find the moment of inertia and the radius of gyration w.r.t. the origin (0,0) of a system which has masses at the points given:
| Mass | `6` | `5` | `9` | `2` |
| Point | `(-3, 0)` | `(-2, 0)` | `(1, 0)` | `(8, 0)` |
Answer
The moment of inertia is:
I = 6(-3)2 + 5(-2)2 + 9(1)2 + 2(8)2
= 54 + 20 + 9 + 128
= 211
To find R, we use:
I = (m1 + m2 + m3 ... + mn)R2
211 = (6 + 5 + 9 + 2)R2
So `R ≈ 3.097`
This means a mass of `22` units placed at `(3.1, 0)` would have the same rotational inertia about O as the 4 objects.
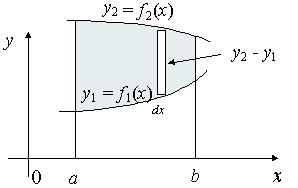
Moment of Inertia for Areas
We want to find the moment of inertia, Iy of the given area, which is rotating around the y-axis.
Each "typical" rectangle indicated has width dx and height y2 − y1, so its area is (y2 − y1)dx.
If k is the mass per unit area, then each typical rectangle has mass k(y2 − y1)dx.
The moment of inertia for each typical rectangle is [k(y2 − y1)dx] x2, since each rectangle is x units from the y-axis.
We can add the moments of inertia for all the typical rectangles making up the area using integration:
`I_y=kint_a^bx^2(y_2-y_1)dx`
Using a similar process that we used for the collection of particles above, the radius of gyration Ry is given by:
`R_y=sqrt((I_y)/m`
where m is the mass of the area.
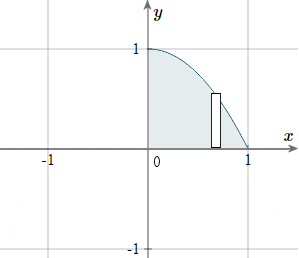
Example 2
For the first quadrant area bounded by the curve
`y = 1 − x^2`,
find:
a) The moment of inertia w.r.t the y axis. (Iy)
b) The mass of the area
c) Hence, find the radius of gyration
Answer
As usual, first we sketch the part of the curve in the first quadrant. It's a parabola, passing through (1, 1) and (0, 1). A "typical" rectangle is shown.
In this example,
`y_2= 1 − x^2`, and `y_1= 0`, `a = 0` and `b = 1`.
a) Finding Iy:
`I_y=k int_a^b x^2(y_2-y_1) dx`
`=k int_0^1x^2 [(1-x^2)-(0)] dx`
`=k int_0^1 [x^2-x^4] dx`
`=k[(x^3)/(3) - (x^5)/(5)]_0^1`
`=k(1/3-1/5)`
`= (2k)/15`
b) The mass of the area, m.
Now m = kA, where A is the area.
Now
`A=int_0^1 (1-x^2) dx`
`=[x-(x^3)/(3)]_0^1`
`=1-1/3`
` = 2/3`
So `m = kA = (2k)/3`
c) The radius of gyration:
`R_y=sqrt{(I_y)/(m)}`
`=sqrt{(2k//15)/(2k//3)}`
`=sqrt[1/5]`
` approx 0.447`
This means that if a mass of `(2k)/3` was placed `0.447` units from the `y`-axis, this would have the same moment of inertia as the original shape.
Rotation about the x-axis
For rotation about the x-axis, the moment of inertia formulae become:
`I_x=kint_c^(d)y^2(x_2-x_1)dy`
and
`R_x=sqrt((I_x)/m`
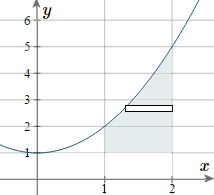
Example 3
Find the moment of inertia and the radius of gyration for the area `y=x^2+1` from `x=1` to `x=2`, and `y>1`, when rotated around the x-axis. The mass per unit area is `3` kg m−2.
Answer
We sketch the parabola. The shaded area is the part that's rotating around the `x`-axis, and we have indicated a "typical" rectangle.
In this example, we are rotating the area around the `x`-axis. We need to express our function in terms of `y`.
Since we started with `y=x^2+1`, we solve for `x` and obtain:
`x=sqrt(y-1)`
We take the positive case only, as we are dealing with the first quadrant.
So the required values which we can use in the formula are:
`x_2= 2` (the "curve" furthest from the `y`-axis),
`x_1= sqrt(y-1)` (the curve closest to the `y`-axis), and
`c = 1` and `d = 5`; and `k=3`.
a) Finding Ix:
`I_x=k int_c^d y^2(x_2-x_1) dy`
`=3 int_1^5 y^2 [(2) - sqrt(y-1)] dy`
`=3 int_2^5 (2 y^2 - y^2 sqrt(y-1)) dy`
We use a computer algebra system to obtain:
`=45.5` kg m2
b) Now to find the mass of the area, m.
m = kA, where A is the area.
Now
`A=int_1^2 (x^2+1) dx - 1` (We need to subtract the area of the `1xx1=1` square below the shaded area.)
`=[(x^3)/(3)+x]_1^2 - 1`
`=(8/3+2)-(1/3+1) - 1`
` = 7/3`
So `m = kA = 3xx7/3 = 7` kg
c) The radius of gyration:
`R_x=sqrt{(I_x)/(m)}`
`=sqrt{(45.5)/(7)}`
` ~~ 2.6` m
This means that if a single mass of `7` kg was placed `2.6` m from the `x`-axis, this would have the same moment of inertia as the original shape when rotating around the `x`-axis.