11. Arc Length of a Curve using Integration
by M. Bourne
Example 1 - Corrugated iron sheeting
Corrugated iron is used extensively throughout the world as a versatile building material. Bending the material into a regular wave pattern gives it greater strength than if a flat sheet is used.
Another example of a light, thin and weak sheet that is made much stronger by having regular folds is corrugated cardboard, used for protecting goods in transit.

The flat sheet is rolled into corrugations, and will be narrower.
To make corrugated iron, you need to bend a wide flat sheet into waves. The resulting corrugated sheet is then narrower, of course.
The corrugations are commonly in the form of a sine curve.
We take a real example of a 4.2" Corrugated Metal Panel, which is a "high profile, wavy style corrugated panel that can be used in almost any roofing, siding, or decorative application." [Source]
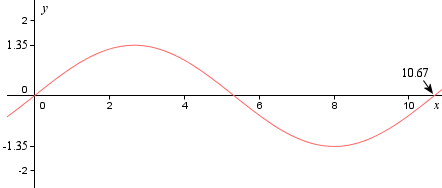
This panel has a finished width of 106.7 cm, a period of 10.67 cm (distance from the top of each wave to the top of the next), and has amplitude 1.35 cm (height from the mid-point of the wave to the top of a crest).
How wide should the flat sheet be to give us a corrugated sheet of width 106.7 cm?
Example 1 Solution
We model the corrugations using the curve
y = 1.35 sin 0.589x
This has the required amplitude 1.35 and period 10.67.
(Within the sine expression, we use 2π/10.67 = 0.589 for the coefficient of x. For background on this, see Period of a sine curve.)
We'll find the width needed for one wave, then multiply by the number of waves.
Approximate answer: Next, let's approximate the length of the curve so we've got a rough idea what our exact length should be. (It's always good practice to estimate your answer first, and in this topic, it helps us understand the concept better).
We plot the points O (0, 0), A (2.65, 1.35), B (5.33, 0), C (7.99, -1.35) and D (10.65, 0), which are key points on the curve (at the mid-points, maximum and minimum values), and join the line segments.
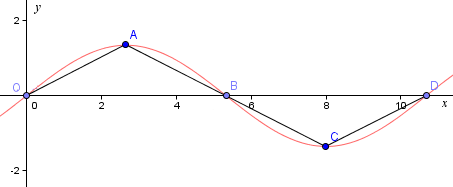
We then use Pythagoras' Theorem to find the length OA:
`OA=sqrt(2.65^2+1.35^2)=2.97`
The distances AB, BC, CD are all equal, so we can say:
OA + AB + BC + CD = 4 × 2.97 = 11.88
So we expect the curved distance OD to be around 12 cm.
Exact value
We'll use calculus to find the 'exact' value. But first, some background.
We zoom in near the center of the segment OA and we see the curve is almost straight.
For this portion, the curve EF is getting quite close to the straight line segment EF.
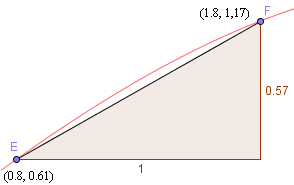
For this zoomed-in section, we have:
curved length EF `= r ≈ int_a^bsqrt(1^2+0.57^2)=1.15`
Of course, the real curved length is slightly more than 1.15.
Let's generalise this.
General Form of the Length of a Curve
If the horizontal distance is "dx" (or "a small change in x") and the vertical height of the triangle is "dy" (or "a small change in y") then the length of the curved arc "dr" is approximated as:
`dr~~sqrt(dx^2+dy^2`
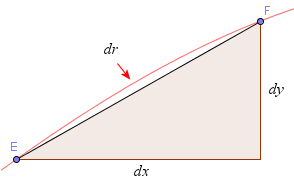
Now, if we move point E very close to point F, we will have a very good approximation for the length of the curve in that local region.
We need to add all those infinitesimally small lengths. We use integration, as it represents the sum of such infinitely small distances. We have for the distance between where `x = a` to `x = b`:
`"length"=r=int_a^bsqrt((dx)^2+(dy)^2`
By performing simple surd manipulation, we can express this in a more familiar form as follows.
The arc length of the curve y = f(x) from x = a to x = b is given by:
`"length"=r=int_a^bsqrt(1+((dy)/(dx))^2)dx`
Of course, we are assuming the function `y = f(x)` is continuous in the region `x = a` to `x = b` (otherwise, the formula won't work).
Back to the Width of the Sheet example
Use the above formula to find the required width of the metal sheet in our example.
Answer
We can now use this formula to find the required width of our flat sheet of iron. Remember, we're finding the width needed for one wave, then we'll multiply by the number of waves.
In our example,
y = 1.35 sin 0.589x, so
`(dy)/(dx)=0.795\ cos\ 0.589x`
For one period, the lower limit is x = 0 and the upper limit is x = 10.67. Substituting these into our formula gives us one wavelength of the curved material:
`r` `=int_0^10.67 sqrt(1+(0.795\ cos\ 0.589x)^2\) dx` `=12.196`
(You can see where this answer comes from in Wolfram|Alpha.)
The corrugated sheet has `(106.7)/(10.67)=10` complete wavelengths across its width, so to give a corrugated width of `106.7\ "cm"`, the original flat sheet will need to be:
`10 × 12.196 = 122.0\ "cm"` wide.
Example 2 - Parabolic dish application
The cross section of a parabolic dish is modelled by y = 0.04x2 (in meters), from x = −5 m to x = 5 m. We need to construct a steel support band which is to be placed around the outer edge of the dish. How long should we make the steel band?
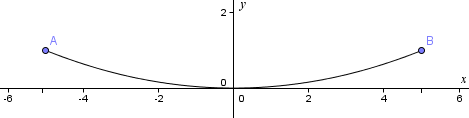
We need to find the curved distance AB.
Answer
Estimate: Looking at the graph (which has equal scaling along the x- and y-axes), we can see the final answer should be a little more than 10 m, somewhere between 10 m and 11 m.
Now to find the exact length:
`text[length]=r=int_a^b sqrt[1+((dy)/(dx))^2]\ dx`
In this example,
y = 0.04x2, so
`(dy)/(dx)=0.08x`
The lower limit is x = −5 and the upper limit is x = 5. Substituting these into our formula gives:
`r=int_-5^5 sqrt(1+(0.08x)^2)\ dx` `= 10.261`
[Note: I used a computer algebra system to find the above integral. Many arc length problems lead to impossible integrals. (This example does have a solution, but it is not straightforward.) Often the only way to solve arc length problems is to do them numerically, or using a computer. You can see the answer in Wolfram|Alpha.]
So the length of the steel supporting band should be 10.26 m.
This is consistent with our earlier estimate.
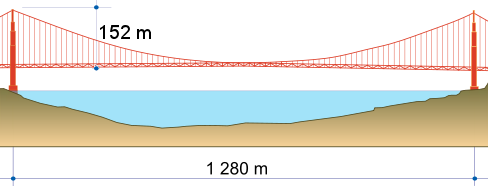
Example 3 - Golden Gate Bridge cables
The central span of the Golden Gate Bridge in San Francisco, USA, is `1280\ "m"` long.
The height of the tower is `152\ "m"` from the roadway. What is the length of the main suspension cable between the 2 towers?
Answer
We first need to model the curve (find an equation that represents the curve accurately).
A freely hanging cable takes the form of a catenary. In the case of a suspension bridge, we need to also consider the mass of the roadway, which will give us a flattened catenary. The general form for a flattened catenary is the sum of 2 exponential functions, based on the hyperbolic function `y=cosh x`:
`y=(a(e^[bx]+e^[-bx]))/(2)`
The Golden Gate Bridge cable is almost a catenary and almost a parabola, but not quite either (because of the weight of the cables, the suspender ropes and the roadway). For the sake of this discussion, we'll assume it is a flattened catenary.
For convenience, we'll place the origin at the lowest point of the cable.
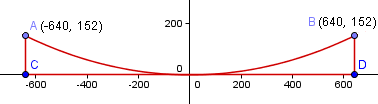
The required curve (after initial analysis and some guess and check) passing through (-640, 152), (0, 0) and (640, 152) is given by:
`y=1280((e^[x//1326]+e^[-x//1326])/(2)-1)`
Here is the graph of the above equation. We can see it passes through the required points.
The derivative of our function is
`(dy)/(dx)=640/663((e^[x//1326]+e^[-x//1326])/(2))`
Using the length of a curve formula, with start point x = -640 and end point x = 640, we have:
`int_-640^640 sqrt[1+(640/663(e^[x/1326]+e^[-x/1326])/(2))^2] dx` ` = 1326.956`
So the length of the central span of the main cable is `1327.0\ "m"`. (You can see the answer in Wolfram|Alpha here.)
Of course, the cable continues on both sides of the towers. The total length of each cable is `2,332\ "m"`.
Interesting trivia: The main cables of the Golden Gate Bridge are nearly one meter in diameter (actually, 0.91 m) and the "total length of galvanized steel wire used in both main cables is 129,000 km". [Source]