6. Simpson's Rule
by M. Bourne
Interactive exploration
See an applet where you can explore Simpson's Rule and other numerical techniques:
In the last section, Trapezoidal Rule, we used straight lines to model a curve and learned that it was an improvement over using rectangles for finding areas under curves because we had much less "missing" from each segment.
We seek an even better approximation for the area under a curve.
In Simpson's Rule, we will use parabolas to approximate each part of the curve. This proves to be very efficient since it's generally more accurate than the other numerical methods we've seen. (See more about Parabolas.)
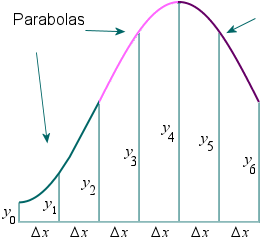
We divide the area into `n` equal segments of width `Delta x`. The approximate area is given by the following.
Simpson's Rule
Area `=int_a^bf(x)dx`
`~~(Deltax)/3(y_0+4y_1+2y_2+4y_3+2y_4+` `{:...+4y_(n-1)+y_n) `
where `Deltax = (b-a)/n`
Note: In Simpson's Rule, n must be EVEN.
See below how we obtain Simpson's Rule by finding the area under each parabola and adding the areas.
Memory aid
We can re-write Simpson's Rule by grouping it as follows:
`int_a^bf(x)dx` `~~(Deltax)/3[y_0+4(y_1+y_3+y_5+...)` `{:+2(y_2+y_4+y_6+...)+y_n]`
This gives us an easy way to remember Simpson's Rule:
`int_a^bf(x)dx` `~~(Deltax)/3["FIRST"+4("sum of ODDs")` `{:+2("sum of EVENs")+"LAST"]`
Example using Simpson's Rule
Approximate `int_2^3(dx)/(x+1)` using Simpson's Rule with `n=4`.
We haven't seen how to integrate this using algebraic processes yet, but we can use Simpson's Rule to get a good approximation for the value.
Answer
Here is the situation.
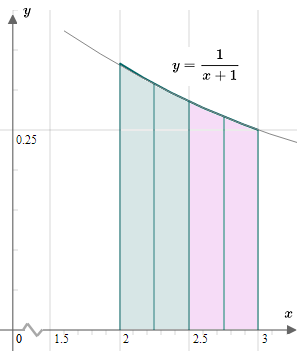
`Δx = (b − a)/n = (3 − 2)/4 = 0.25`
`y_0= f(a)`
` = f(2)`
`= 1/(2 + 1) = 0.3333333 `
`y_1= f(a + Δx) = f(2.25)` `= 1/(2.25+1) = 0.3076923`
`y_2= f(a + 2Δx) = f(2.5)` `= 1/(2.5+1) = 0.2857142`
`y_3= f(a + 3Δx) = f(2.75)` `= 1/(2.75+1) = 0.2666667`
`y_4= f(b) = f(3)` `= 1/(3+1) = 0.25`
So
Area ` = int_a^bf(x) text[d]x`
`approx 0.25/3 (0.333333+4(0.3076923)` `+2(0.2857142)+4(0.2666667)` `{:+0.25)`
`=0.2876831`
Notes
1. The actual answer to this problem is 0.287682 (to 6 decimal places) so our Simpson's Rule approximation has an error of only 0.00036%.
2. In this example, the curve is very nearly parabolic, so the 2 parabolas shown above practically merge with the curve `y=1/(x+1)`.
Don't miss...
There is an interactive applet where you can explore Simpson's Rule, here:
Calculus from First Principles applet
Background and proof for Simpson's Rule
We aim to find the area under the following general curve.
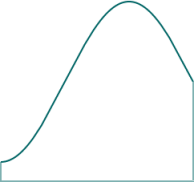
We divide it into 4 equal segments. (It must be an even number of segments for Simpson's Rule to work.)
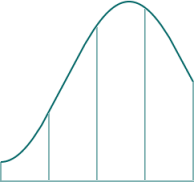
We next construct parabolas which very nearly match the curve in each of the 4 segments. If we are given 3 points, we can pass a unique parabola through those points.
NOTE: We don't actually need to construct these parabolas when applying Simpson's Rule. This section is just to give you some background on why and how it works.
Let's start with the first 2 segments on the left. We take the end points, and the middle point as shown:
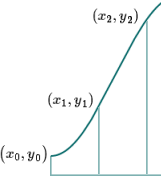
We can take measurements (using an overlaid grid) and observe these three points to be:
`(x_0,y_0) = (−1.57, 1)`
`(x_1,y_1) = (−0.39, 1.62)`
`(x_2,y_2) = (0.79, 2.71)`
Using these 3 points, we use the general form of a parabola, `y=ax^2+bx+c`, and substitute the known `x`- and `y`-values, as follows.
`1=a(-1.57)^2+b(-1.57)+c`
`1.62=a(-0.39)^2+b(-0.39)+c`
`2.71=a(0.79)^2+b(0.79)+c`
This gives us a set of 3 simultaneous equations in 3 unknowns, which we can solve using these algebraic methods. Doing so gives us:
`a=0.17021`, `b=0.85820`, `c=1.92808`.
So the parabola passing through those 3 points is
`y=0.170x^2+0.858x+1.93`
Note: Of course, we are using full calculator accuracy throughout, but final results are rounded.
Here is what that parabola looks like:
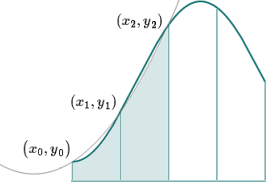
We can see the parabola passes through the 3 points, and it is close to our original curve, and so it's a good approximation for the curve in that portion of the graph. As usual, the more divisions we take, the more accurate it will be.
We do the same process for the final 2 segments, and get a parabola that passes through the 3 points shown, and which looks like this:
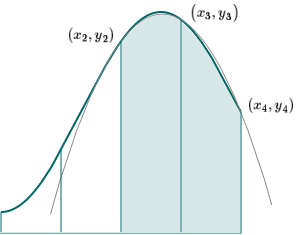
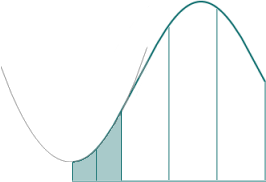
There are noticeable gaps between the oriignal curve and our parabolas. We only have to halve the segment size to get a much better fit, as we can see in this next image. The parabola is almost identical to the curve.
See an applet that explores this concept here:
Proof of Simpson's Rule
We consider the area under the general parabola `y=ax^2+bc+c`.
For easier algebra, we start at the point `(0,y_1)`, and consider the area under the parabola between `x=-h` and `x=h`, as shown. (Note that `Delta x = h`.)
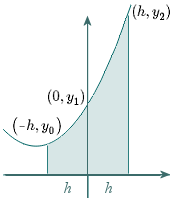
We have:
`int_(-h)^h (ax^2+bx+c)\ dx `
`= [(ax^3)/3 + (bx^2)/2 + cx]_(-h)^h `
`= ((ah^3)/3 + (bh^2)/2 + ch)-` `(-(ah^3)/3 + (bh^2)/2 - ch) `
`= (2ah^3)/3 + 2ch`
`=h/3(2ah^2 + 6c)` (getting it into a convenient form)
Our parabola passes through `(-h,y_0)`, `(0,y_1)`, and `(h,y_2)`. Substituting these `x`- and `y`-values into the general equation of our parabola, we get:
` y_0 = ah^2 - bh + c`
`y_1 = c`
`y_2 = ah^2 + bh +c`
Solving these gives us
`c = y_1` (from the second line)
and
`2ah^2 = y_0 -2y_1 + y_2` (by adding the first and 3rd line)
Substituting these into `A = h/3(2ah^2 + 6c)` from above, we have:
`A = h/3(2ah^2 + 6c)`
`= h/3(y_0 -2y_1 + y2 + 6y_1)`
`= h/3(y_0 + 4y_1 + y_2)`
The parabola passing through the next set of 3 points will have an area of:
`A = h/3(y_2 + 4y_3 + y_4)`
Adding the 2 areas, we get:
`A= h/3(y_0 + 4y_1 + 2y_2 + 4y_3 + y_4)`
Say we have 6 subintervals. We just find the areas under the 3 resulting parabolas, and add them to obtain:
`A = h/3[y_0 + 4y_1 + 2y_2 + 4y_3 +` ` 2y_4 +` ` 4y_5 +` `{: y_6]`
We could keep going by creating more and more segments, and adding the areas as we go along. and we would obtain Simpson's Rule:
`int_a^bf(x)dx` `~~(Deltax)/3(y_0+4y_1+2y_2+4y_3+` `2y_4...+` `4y_(n-1)+` `{:y_n) `
Problem Solver
Need help solving a different Calculus problem? Try the Problem Solver.
Disclaimer: IntMath.com does not guarantee the accuracy of results. Problem Solver provided by Mathway.