3. Double-Angle Formulas
by M. Bourne
The double-angle formulas can be quite useful when we need to simplify complicated trigonometric expressions later.
With these formulas, it is better to remember where they come from, rather than trying to remember the actual formulas. In this way, you will understand it better and have less to clutter your memory with.
Sine of a Double Angle
sin 2α = 2 sin α cos α
Proof
Recall from the last section, the sine of the sum of two angles:
sin(α + β) = sin α cos β + cos α sin β
We will use this to obtain the sine of a double angle.
If we take the left hand side (LHS):
sin(α + β)
and replace β with α, we get:
sin(α + β) = sin(α + α) = sin 2α
Consider the RHS:
sin α cos β + cos α sin β
Since we replaced β in the LHS with α, we need to do the same on the right side. We do this, and obtain:
sin α cos α + cos α sin α = 2 sin α cos α
Putting our results for the LHS and RHS together, we obtain the important result:
sin 2α = 2 sin α cos α
This result is called the sine of a double angle. It is useful for simplifying expressions later.
Cosine of a Double Angle
Using a similar process, we obtain the cosine of a double angle formula:
cos 2α = cos2 α − sin2 α
Proof
This time we start with the cosine of the sum of two angles:
cos(α + β) = cos α cos β − sin α sin β,
and once again replace β with α on both the LHS and RHS, as follows:
LHS = cos(α + α) = cos(2α)
RHS = cos α cos α − sin α sin α = cos2 α − sin2 α
Different forms of the Cosine Double Angle Result
By using the result sin2 α + cos2 α = 1, (which we found in Trigonometric Identities) we can write the RHS of the above formula as:
cos2 α − sin2 α
= (1− sin2 α) − sin2 α
= 1− 2sin2 α
Likewise, we can substitute (1 − cos 2 α) for sin2 α into our RHS and obtain:
cos2 α − sin2 α
= cos2 α − (1 − cos2 α)
= 2cos2 α − 1
Summary - Cosine of a Double Angle
The following have equivalent value, and we can use whichever one we like, depending on the situation:
cos 2α = cos2 α − sin2 α
cos 2α = 1− 2 sin2 α
cos 2α = 2 cos2 α − 1
Example 1
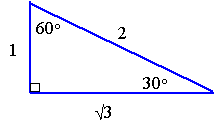
Find cos 60° by using the functions of 30°.
Answer
We can only use the sine and cosine functions of `30^"o"`, so we need to start with `60^"o" = 2 × 30^"o"`.
We will use the result
cos 2α = cos2 α − sin2 α,
and the 30-60 triangle:
Now we proceed to find the exact value of cos60° using the ratios of 30°:
`cos 60^text(o)=cos(2xx30^text(o))`
`=cos^2(30^text(o))-sin^2(30^text(o))`
`=(sqrt3/2)^2-(1/2)^2`
`=3/4-1/4`
`=2/4`
`=1/2`
These exercises are really here for practice on the double angle formula. Of course, we could have found the value of cos60° directly from the triangle.
Example 2
Find the exact value of `cos 2x` if `sin x= -12/13` (in Quadrant III).
Answer
Using the following form of the cosine of a double angle formula, cos 2α = 1− 2sin2 α, we have:
`cos 2x=1-2 sin^2x`
`=1-2((-12)/13)^2`
`=1-2(144/169)`
`=(169-288)/169`
`=(-119)/169`
Notice that we didn't find the value of x using calculator first, and then find the required value. If we had done that, we would not have found the exact value, and we would have missed the pleasure of seeing the double angle formula in action :-)
Exercises
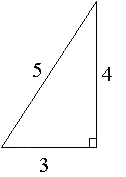
1. Without finding `x`, find the exact value of `sin 2x` if `cos x= 4/5` (in Quadrant I).
Answer
We recognise that we need to use the 3-4-5 triangle (because of the 4 and 5 in the question).
We can use our formula for the sine of a double angle to find the required value:
`sin 2x=2 sin x cos x`
`=2(3/5)(4/5)`
`=24/25`
2. Prove that
`(1-tan^2x)/(sec^2x)=cos2x`
Answer
When we need to prove an identity, we start on one side (usually the most complicated side) and work on it until it is equivalent to the other side.
In this example, we start on the left hand side and use our various identities from earlier sections to simplify it.
`"LHS"=(1-tan^2x)/(sec^2x)`
`=1/(sec^2x)(1-tan^2x)`
`=cos^2x(1-(sin^2x)/(cos^2x))`
`=cos^2x xx(cos^2x-sin^2x)/(cos^2x)`
`=cos^2x-sin^2x`
`=cos 2 x`
`="RHS"`
3. Prove that
`2 csc 2x tan x = sec^2x`
Answer
A good approach with these proofs is to reduce everything to sine and cosine only. Then you find the steps are easier to simplify, and it is easier to recognise the various formulas we have learned.
`"LHS"=2 csc 2x tan x`
`=(2 tan x)/(sin 2x)`
`=(2 tan x)/(2 sin x cos x)`
`=(sin x)/(cos x)xx1/(sin x cos x)`
`=1/(cos^2x)`
`=sec^2x`
`="RHS"`