5. Signs of the Trigonometric Functions

by M. Bourne

Angles greater than 90°

We define the trigonometric functions for angles greater than 90° in the following way:

By Pythagoras, `r=sqrt(x^2+y^2`. Then the ratios are:

How is this different to the definitions we already met in section 2, Sine, Cosine, Tangent and the Reciprocal Ratios? The only difference is that now x or y (or both) can be negative because our angle can now be in any quadrant. It follows that the trigonometric ratios can turn out to be negative or positive. In the earlier section, the angles involved were always less than 90° so all 6 ratios were positive.

Notice that r is always positive.

Example 1

Let's see how the trigonometric ratios are defined using a particular example. Let our angle θ be defined by the point `(-2,3)` in the following way:

By Pythagoras,

`r=sqrt(x^2+y^2)` `=sqrt((-2)^2+3^2)` `=sqrt(4+9)=sqrt13`

For this example, we define the trigonometric ratios for θ in the following way:

The Four Quadrants - Positive or Negative?

Observe for the example above, that our angle was in the second quadrant. Also notice that in the second quadrant, the y-value is positive. Since r is always positive, then `y/r` will always be positive in quadrant II. So we conclude `sin theta` is always going to be positive in the second quadrant.

Also observe for (in the `cos theta` case) , that x was negative. In the second quadrant, x is always negative. So `cos theta` will always be negative there, too.

For the `tan theta` case, y is positive and x is negative, so `y/x` will always be negative.

Considering the other quadrants, we see a pattern.

In Quadrant II, `sin theta` is positive, `cos theta` and `tan theta` are negative.

In Quadrant III, `tan theta` is positive (both x and y are negative, so `y/x` is positive), `sin theta` and `cos theta` are negative.

In Quadrant IV, `cos theta` is positive, `sin theta` and `tan theta` are negative.

Of course the reciprocal ratios, `csc theta`, `sec theta` and `cot theta` follow the same pattern:

In Quadrant II, `csc theta` is positive, `sec theta` and `cot theta` are negative.

In Quadrant III, `cot theta` is positive, `csc theta` and `sec theta` are negative.

In Quadrant IV, `sec theta` is positive, `csc theta` and `cot theta` are negative.

We don't need to remember the reciprocal ones off by heart, but it is recommended that you remember where `sin theta`, `cos theta` and `tan theta` are positive.

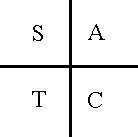
We use this diagram to remember what ratios are positive in each quadrant. We can remember it using:

All Stations To Central.

It means: In the first quadrant (I), all ratios are positive.

In the second quadrant (II), sine (and cosec) are positive.

In the third quadrant (III), tan (and cotan) are positive.

In the fourth quadrant (IV), cos (and sec) are positive.

These just follow from the sign (+ or -) of x or y for each quadrant, as we saw above.

These signs are important when we are finding an angle from a given ratio.

Interactive graph

Here's an interactive graph where you can explore trigonometric ratio concepts.

Drag the point P around the curve into all 4 quadrants and observe the sin, cos and tan ratios that result. Notice in particular the ratios which are positive in each quadrant.

Also, note that `sin theta` is defined as `y/r`, and `cos theta` is defined as `x/r` and `tan theta` is defined as `y/x`.

This is where the positive and negative values come from, and it's just an extension of the ratios we learned earlier, when `theta` was restricted to being less than `90°`.

Examples 2

What is the sign (+ or −) of the following?

a. `sin 50^@`

b. `cos 100^@`

c. `tan 200^@`

d. `csc 300^@`

Do these without calculator so that you have a better idea what is going on.

Answer

Exercises

1. What is the sign (+ or −) of the following?

a) `sin(100^@)`

b) `sec(-15^@)`

c) `cos(188^@)`

Answer

2. Find the trigonometric ratios of the angle with terminal side at `(-3,-4)`.

Answer