4. The Right Triangle and Applications
Many problems involve right triangles. We often need to use the trigonometric ratios to solve such problems.
Example 1 - Finding the Height
Find h for the given triangle.
Answer
`sin 15.70^"o" = h/2.500`
`h = 2.500\ sin 15.70^"o"`
`= 0.6765\ "km"`
Example 2 - Solving Triangles
Solve the triangle ABC, given that `A = 35°` and `c = 15.67`.
Answer
To "solve" a triangle means to find the unknown sides and angles.
We have, for the values given:
In this example, we need to find side lengths a and b and angle B. Note C = 90o.
`sin 35^"o" = a/c = a/15.67`
So a = 15.67 sin 35o = 8.99
`cos 35^"o"=b/c=b/15.67`
So b = 15.67 cos 35o = 12.84
Angle B = 90o − 35o = 55o.
So a = 8.99, b = 12.84 and B = 55o. We have found all the unknowns.
Angles of Elevation and Depression
In surveying, the angle of elevation is the angle from the horizontal looking up to some object:
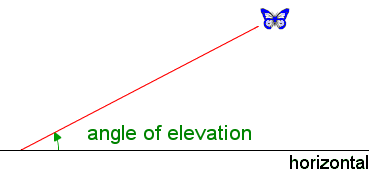
The angle of depression is the angle from the horizontal looking down to some object:

Example 3
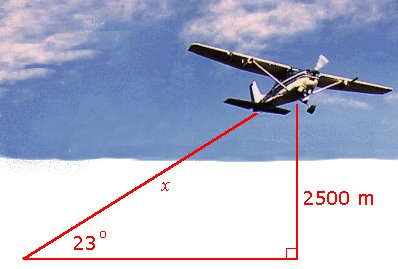
The angle of elevation of an aeroplane is `23°`. If the aeroplane's altitude is `2500\ "m"`, how far away is it?
Answer
Let the distance be x. Then `sin 23^"o"=2500/x`
`x=2500/(sin 23^"o")=6400\ "m"`
Example 4
You can walk across the Sydney Harbour Bridge and take a photo of the Opera House from about the same height as top of the highest sail.

This photo was taken from a point about `500\ "m"` horizontally from the Opera House and we observe the waterline below the highest sail as having an angle of depression of `8°`. How high above sea level is the highest sail of the Opera House?
Answer

This is a simple tan ratio problem.
`tan 8^"o" = h/500`
So
`h= 500\ tan 8° = 70.27\ "m"`.
So the height of the tallest point is around `70\ "m"`.
[The actual height is `67.4\ "m"`.]