Home | Math Display Experiments | Curve Shape for the Movement of a Piston

Curve Shape for the Movement of a Piston

When a piston moves through a cylinder the resulting motion is almost sinusoidal if the crank has a small radius compared to the length of the rod.

However, if the crank radius is large compared to the rod length, the curve shape is not at all sinusoidal.

This applet allows you to explore this concept.

Piston parts

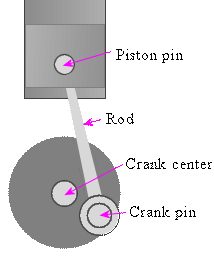
We represent the distances and points involved as follows:

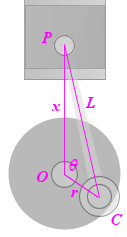
`L` is the (fixed) length of the rod

`x` is the distance from the center of the crank (`O`) and the piston pin (`P`).

`r` is the distance `OC`.

`theta` is the angle `/_POC`.

Now, using the Cosine Rule from basic trigonometry, we have:

`L^2 = r^2 + x^2 - 2rx cos(theta)`

Solving this for `x`, and using the fact `cos^2 theta = 1 - sin^2 theta`, we get the following, which is the equation for the movement of a piston driven by a circular crank:

`x=rcosA+sqrt(L^2-r^2sin^2 theta)`

We can see from this last equation that if `L` is large compared to `r`, the expression under the square root becomes close to `sqrt(L^2) = L` (a constant), and the motion will be close to `x=rcosA+L`, which is sinusoidal.

The piston applet

In this applet, the lighter colored curve is a "pure" sine curve. You can see how the darker curve is not quite the same.

Change the sliders to vary the crank radius and the rod length.

See what happens when amplitude = rod length.

Of course, this is not representative of a realistic engine. If the amplitude is very close to the rod length, the engine would freeze.

Back to Experiments page.