2. Antiderivatives and The Indefinite Integral
by M. Bourne
Mini-Lecture
See the
mini-lecture on differentials
We wish to perform the opposite process to differentiation. This is called "antidifferentiation" and later, we will call it "integration".
Example 1
If we know that
`(dy)/(dx)=3x^2`
and we need to know the function this derivative came from, then we "undo" the differentiation process. (Think: "What would I have to differentiate to get this result?")
`y = x^3` is ONE antiderivative of `(dy)/(dx)=3x^2`
There are infinitely many other antiderivatives which would also work, for example:
`y = x^3+4`
`y = x^3+pi`
`y = x^3+27.3`
In general, we say `y = x^3+K` is the indefinite integral of `3x^2`. The number K is called the constant of integration.
Note: Most math text books use `C` for the constant of integration, but for questions involving electrical engineering, we prefer to write "+K", since C is normally used for capacitance and it can get confusing.
Notation for the Indefinite Integral
We write: `int3x^2dx=x^3+K` and say in words:
"The integral of 3x2 with respect to x equals x3 + K."
The Integral Sign
The `int` sign is an elongated "S", standing for "sum". (In old German, and English, "s" was often written using this elongated shape.) Later we will see that the integral is the sum of the areas of infinitesimally thin rectangles.
`sum` is the symbol for "sum". It can be used for finite or infinite sums.
`int` is the symbol for the sum of an infinite number of infinitely small areas (or other variables).
This "long s" notation was introduced by Leibniz when he developed the concepts of integration.
Other Notation for Integrals
Note: Sometimes we write a capital letter to signify integration. For example, we write F(x) to mean the integral of f(x). So we have:
`F(x)=intf(x)dx`
Example 2
Find `int(x^2-5)dx`
Answer
The antiderivative of `x^2` is `x^3/3`, and the antiderivative of `5` is `5x`, so we can write:
`int (x^2-5) dx = frac{x^3}{3}-5x+K`
We now learn some important general rules for integration.
A. Integral of a Constant
`intk dx=kx+K`
(`k` and `K` are constants.)
The integral of a constant is that constant times x, plus a constant.
Example 3
Find `int4 dx`
Answer
Using our new rule, we can simply write:
`int4 dx=4x+K`
Always check by differentiating your answer, and you should get back to what the question was asking you to integrate.
B. Integral of a Power of x
`intx^ndx=(x^(n+1))/(n+1)+K` (This is true as long as `n ≠ -1`)
For the integral of a power of x: add 1 to the power and divide by the new number.
Example 4
Integrate `intx^5 dx`
Answer
We use our new rule, and obtain:
`intx^5 dx=(x^(5+1))/(5+1)+K`
`=x^6/6+K`
The Constant of Integration
Don't forget the "+ K" (or, alternatively, "+ C"). This constant of integration is vital in later applications of the indefinite integral.
Example 5
Integrate `int 8x^6 dx`
Answer
`int 8x^6 dx`
`8` is a constant, so it can go out the front:
`8 int x^6 dx`
Next, do the integration step by adding 1 to the index and dividing by the new number:
`8 x^(6+1)/(6+1) = 8(x^7)/7`
And of course, we must not forget the constant.
So the final answer is:
`int 8x^6 dx = 8(x^7)/7+K`
Example 6
Integrate `dy = (5x^2 - 4x + 3)dx`
Answer
`dy = (5x^2 - 4x + 3)dx`
This is already in differential form, so we can just add the integral signs:
`int dy = int(5x^2 - 4x + 3)dx`
On the left hand side, we simply have:
`int dy = int(1)dy = y` (We are integrating the constant `1` with respect to `y`.)
On the right hand side, we integrate each of the terms, one at a time:
`int(5x^2 - 4x + 3)dx = 5(x^3)/3-4(x^2/2)+3x+K`
`=5(x^3)/3-2x^2+3x+K`
So putting it all together, we have the solution:
`y=5(x^3)/3-2x^2+3x+K`
Example 7
`int7x^6dx`
Answer
`int 7x^6 dx = 7 frac{x^7}{7}+K`
` = x^7+K`
Example 8
`int(3x^2+sqrtx-5/x^3)dx`
Answer
Our first step in this question is to re-write the exponents so it is easier to integrate:
`int (3x^2 + sqrt[x] - frac{5}{x^3})dx = int (3x^2+x^[frac{1}{2}]-5x^-3)dx`
`=x^3+frac{x^[frac{3}{2}]}{3/2}-5frac{x^-2}{-2}+K`
`=x^3+frac{2x^[frac{3}{2}]}{3}+frac{5x^-2}{2}+K`
Example 9
`introot(3)(x^2)dx`
Answer
Once again, we re-write the exponents in a more convenient form.
`int root(3)(x^2)dx = intx^(2//3)dx`
`=(x^(2/3+1)/(2/3+1))+K`
`=(x^(5//3))/(5//3)+K`
`=(3root(3)(x^5))/5+K`
Notice the constant of integration, `+K`, in each of these examples.
Example 10
A particular curve has its derivative given by `(dy)/(dx)=3x^2-2x`.
We are told that the curve passes through the point (2, 5). Find the equation of the curve.
Answer
The first step for this problem is to integrate the expression (i.e. find the antiderivative). This will give us the expression for `y`.
`int(3x^2-2x)dx=x^3-x^2+K`
So we have `y = x^3− x^2+ K`
This represents a family of curves, and depends on the value of `K` for the y-intercept.
We must now find the value of `K` from the information given in the question.
Since the curve passes through `(2, 5)`, we substitute these values into
`y = x^3− x^2+ K`
to give:
`5 = (2)^3 − (2)^2 + K`
`5 = 8 − 4 + K`
So `K = 1`.
So the required curve is `y = x^3− x^2+ 1`
Here is a graph of the curve we found in Example 10:
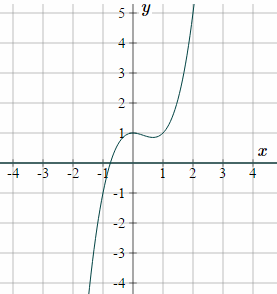
Notice the curve passes through the point `(2,5)`.
Example 11
Consider this integration:
`int(2x^4-5)^6x^3dx`
This is different to the other exercises above!
The expression we have to integrate containts `(2x^4-5)^6`, which is a function of a function, and we have that `x^3` at the end. We cannot do this integration using the rules we have learned so far.
In this case, we have to do the reverse of the Chain Rule, which we met in the section on differentiation.
We introduce a new rule for integrating cases like these.
Mini-Lecture
See the
mini-lecture on substitution.
C. Power Formula for Integration
`int u^ndu=u^(n+1)/(n+1)+K`
(This is true if `n ≠ -1`)
This requires a substitution step, where u(x) is some function of x.
Now back to the problem to see how to apply this formula.
Integrate `int(2x^4-5)^6x^3dx`.
Answer
We use, as a starting point, the substitution
`u = 2x^4- 5`.
Why? Because `2x^4- 5` is the expression in brackets in the question.
Now differentiating `u` gives: `du = 8x^3 dx`
Our question has only one `x^3 dx` (not 8 of them) so we need to divide both sides by `8`:
`1/8du=x^3 dx`
(Now the right hand side is the same as what we have in the question, `x^3 dx`.)
We can now rewrite our question as:
`int(2x^4-5)^6x^3 dx`
`=1/8intu^6 du`
(Notice I'm not mixing up `x`'s and `u`'s in any one expression here.)
Now we integrate with respect to `u`:
`=1/8xxu^7/7+K`
`=u^7/56+K`
Finally, we express everything in terms of `x`, since that's the variable we started with:
`=((2x^4-5)^7)/56+K`
More substitution examples
Example 12
`int(x^3-2)^6(3x^2)dx`
Answer
We use, as a starting point, `u = x^3- 2`.
Now `du = 3x^2 dx`
This time, this is exactly what we have in the question, so there is no need to divide both sides.
We can now write:
`int(x^3-2)^6(3x^2) dx=intu^6 du`
`=u^7/7+K`
`=((x^3-2)^7)/7+K`
Example 13
Find `intx/(sqrt(x^2+9))dx` using a substitution.
Answer
Put `u=x^2+9`
Then `du = 2x dx`
The question has just one `x dx` so we divide both sides by 2:
`(du)/2=x dx`
Now
`intx/sqrt(x^2+9)dx = 1/2int(du)/sqrtu`
`=1/2intu^(-1//2)du`
`=1/2(u^(1//2))/(1//2)+K`
`=u^(1//2)+K`
`=sqrt(x^2+9)+K`
Example 14
Given `y'=sqrt(2x+1`, find the function `y = f(x)` which passes through the point `(0,2)`.
Answer
NOTE: `y'` means the derivative of `y`, that is `(dy)/dx`.
`y'=sqrt(2x+1`
So
`y=intsqrt(2x+1) dx`
This question requires us to integrate, and in the process, to find the constant of integration.
Put `u = 2x + 1`.
Now `du = 2 dx`
So
`1/2du=dx`
So
`y=intsqrt(2x+1) dx`
`=1/2intu^(1//2)du`
`=1/2xx2/3xxu^(3//2)+K`
`=1/3(2x+1)^(3//2)+K`
Now if `x = 0` then `y = 2` (from the question).
`2=(1^(3//2))/3+K`
and this gives `K = 5/3`.
So
`y=((2x+1)^(3//2))/3+5/3`
is the required function.
Here is the graph of the answer we found in Example 14. You can see it passes through (2, 0).
Graph of y, passing through (2, 0).
Note: You will see "+K" and "+C" in this work. Most textbooks use + C.
It's a good idea to always use +K if you are answering electrical problems.