3. Solving Non-linear Inequalities
Another method of solving inequalities is to express the given inequality with zero on the right side and then determine the sign of the resulting function from either side of the root of the function.
The steps are as follows:
- Rewrite the inequality so that there is a zero on the right side.
- Find all linear factors of the function.
- To find the critical values, set each linear function to zero and solve for x.
- Determine the sign of the function in the intervals formed by the critical values.
- The solution will be those intervals in which the function has the correct signs satisfying the inequality.
Example 1
Solve the inequality x2 − 3 > 2x
Answer
First, we rearrange the inequality with a zero on the right:
x2 − 2x − 3 > 0
which can be factored to give:
`(x + 1)(x - 3) > 0`
Setting both factors to zero, we get:
`(x + 1) = 0 and (x - 3) = 0`
`x = -1 and x = 3`
Therefore the critical values are
`x = -1 and x = 3`.
These critical values divide the number line into 3 intervals:
`x < -1`,
`-1 < x < 3`, and
`x > 3`.
Next, we need to determine the sign (plus or minus) of the function in each of the 3 intervals.
For the first interval, `x < -1`,
The value of `(x + 1)` will be negative (substitute a few values of `x` less than `-1` to check),
The value of `(x − 3)` will also be negative
So in the interval `x < -1`, the value of the function x2 − 2x − 3 will be
negative × negative = positive
We continue doing this for the other 2 intervals and summarise the results in this table:
| Interval | `(x + 1)` | `(x - 3)` | sign of f(x) |
| `x < -1` | − | − | + |
| `-1 < x < 3` | + | − | − |
| `x > 3` | + | + | + |
We are solving for
`(x + 1)(x - 3) > 0`
The intervals that satisfy this inequality will be those where f(x) has a positive sign.
Hence, the solution is: `x < -1` or `x > 3`.
Here is the graph of our solution:
Example 2
Solve the inequality x3 − 4x2 + x + 6 < 0
Answer
Using methods learnt in earlier chapters (see Remainder and Factor Theorems), the expression can be factored to give:
(x + 1)(x − 2)(x − 3) < 0
Setting the factors to zero, we get:
(x + 1) = 0
(x − 2) = 0
(x − 3) = 0
So `x = −1`, `x = 2`, or `x = 3`.
Therefore the critical values are
`x = −1`, `x = 2` and `x = 3`.
These critical values divide the number line into 4 intervals:
x < −1,
−1 < x < 2,
2 < x < 3 and
x > 3.
Next, we determine the sign of the function by the following method:
| Interval | `(x + 1)` | `(x − 2)` | `(x − 3)` | sign of f(x) |
| `x < −1` | − | − | − | − |
| `−1 < x < 2` | + | − | − | + |
| `2 < x < 3` | + | + | − | − |
| `x > 3` | + | + | + | + |
Since we want `f(x) < 0`, the intervals that satisfy this inequality will be those with a negative sign.
Hence, the solution is: `x < −1` or `2 < x < 3`.
Here is the graph of our solution:
Example 3
Solve the inequality `((x-2)^2(x+3))/(4-x) < 0`
Answer
The critical values are
`x = −3`, `x = 2` and `x = 4`.
These critical values divide the number line into 4 intervals.
Hence, the signs of the function are:
| Interval | `((x−2)^2(x+3))/(4−x)` | sign of f(x) |
| `x < −3` | 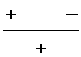 |
− |
| `−3 < x < 2` | 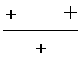 |
+ |
| `2 < x < 4` | 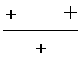 |
+ |
| `x > 4` | 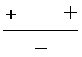 |
− |
Since we want `f(x) < 0`, the intervals that satisfy this inequality will be those with a negative sign.
Hence, the solution is: `x < −3` or `x > 4`.
Here's the graph of the solution.
Exercises
1. Solve `x^3-2x^2+x >= 0`
Answer
`x^3−2x^2+x >= 0`
`x(x^2−2x+1) >= 0`
`x(x−1)^2 >= 0`
Our critical values are: `x=0 or 1`.
Testing as above, we find our solution set is: `x>=0`.
Here's the solution graph:
2. The mass m, in Mg, of fuel in a rocket after launch is
m = 2000 − t2 − 140t
where t is measured in minutes. During what time is the mass of fuel greater than `500\ "Mg"`?
Answer
We need to solve: `2000 − t^2− 140t > 500`.
`1500 − t^2− 140t > 0`
`t^2+ 140t − 1500 < 0`
`(t + 150)(t − 10) < 0`
So ` −150 < t < 10`.
But t cannot be negative, so `0 ≤ t < 10`.
The solution graph is:
3. The object distance p, and the image distance q, for a camera of focal length 3 cm is given by:
`p=(3q)/(q-3)`
For what values of q is p > 12 cm?
Answer
We set up the inequality as follows:
`(3q)/(q−3)>12`
The logical first step would be to multiply both sides by (q − 3). However, we can only do that if (q − 3) is positive. (Otherwise, if (q − 3) is negative, the > sign would need to change to `<`.)
Of course, q ≠ 3, since we cannot have `0` on the bottom of a fraction.
So we have (if q > 3):
3q > 12(q − 3)
Divide both sides by 3:
q > 4(q − 3)
Expand brackets:
q > 4q − 12
Add 12 to both sides and subtract q from both sides:
12 > 4q − q
12 > 3q
4 > q
Reverse sides (and reversing the > sign as well):
q < 4
So including the condition q > 3, our final answer is:
3 < q < 4
The graph of the solution:
