Following is an example of a math mini-project. Students were required to use Scientific Notbebook (or other computer algebra system) to explain an application of integration.
Used with permission.
Return to IntMath
A roller coaster ride begins with an engine hauling a train of cars up to the top of a steep slope and releasing them. From this point on the train is powered by gravity alone and the ride can be analysed by using the fact that as the train drops in elevation, its potential energy is converted into kinetic energy.
We can derive a formula for the time t required for a ride along any curve
that the roller coaster track takes. Below is the details of the analysis.
At the point
in the picture, the potential energy lost is
,
so the kinetic energy at that point is given by :
Solving for v gives us a basic formula :
To find a formula for
,
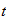we must manipulate the above equation. Rewriting
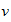in terms of its horizontal and vertical components, let :
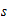represent the accumulated distance along the curve,
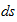represent a small increment distance along the curve,
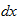and
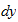represent the horizontal and vertical components of ds.
Therefore :
represents the velocity along the curve,
represents the
component of the velocity,
and
are given by Pythagoras' theorem,
the chain rule gives :
Substituting this into our basic formula :
To find t :
We can use this formula on a roller coaster track with the equation
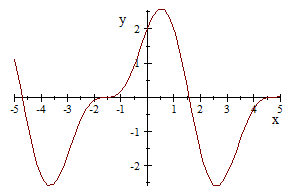
First we differentiate the equation :
To find time taken to travel from 0m to 1m:
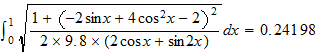
Therefore the time taken to travel fom 0m to 1m is about
In conclusion, we can use this formula on any roller coaster track to find the time taken to travel from one point to another, provided we have an equation of the track and its derivative. We can see how easy it is to solve a complicated problem using integration.
Picture taken from www.calculus.net
Equation of curve taken from Basic Technical Mathematics(Part 1)
Picture taken from www.rcdb.com
Return to IntMath