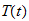changes in a cooling body is proportional to the differences between the
temperature of the body and the constant temperature
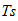of the surrounding medium; this situation is represented as the first_order
initial _value problem
Following is an example of a math mini-project. Students were required to use Scientific Notbebook (or other computer algebra system) to explain an application of differential equations.
Used with permission.
Return to IntMath
First_order linear differential equations can be used to solve a variety of problems that involve temperature .For example:
a medical examiner can find the time of death in a homicide case,
a chemist can determine the time required for a plastic mixture to cool to a hardening temperature
and an engineer can design the cooling and heating system of a manufacturing facility although distinct;
Each of these problems depends on a basic principle that is used to develop the associated differential equation, we discuss this important law now.
basic concept of Newton's law of cooling
Newton's law of cooling states that the rate at which the temperature
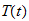changes in a cooling body is proportional to the differences between the
temperature of the body and the constant temperature
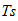of the surrounding medium; this situation is represented as the first_order
initial _value problem
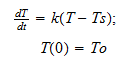
Where
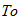is the initial temperature of the body and
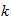is the constant of proportionality; we investigate problems involving Newton's
law of cooling in the following examples
In the ideal case , the temperature of the surroundings was assumed to be constant;
However ,this does not have to be the case ;for example, consider the problem
of heating and cooling a building ;over the span of a twenty-four hour day,
the outside temperature varies ;the problem of determining the temperature
inside the building ,therefore ,becomes more complicated ;for the
meantime,lets's assume that the building has no heating or air conditioning
system ;hence the differential equation that should be solved to find the
temperature
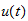at time
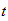inside the building is
Where
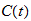is a function that describes the outside temperature and
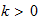is a constant that depends on the insulation of the building; according to
this equation ,if
,then
which
implies that
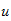increase ;conversely ,if
,then
,which
means that
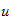decreases.
Example:
(a) suppose that during the
month of April in Atlanta, Georgia, the outside
temperature is given by
,
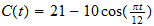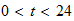;(Note:
this implies that the average value of
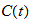is
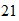
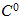) determine the temperature in a building that has an initial temperature of
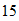
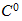if
;
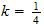(b)compare this to the temperature in June when the
outside temperature is
and
the initial temperature is
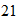
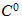
solution: (a)the initial_value problem that
we must solve in April is
,
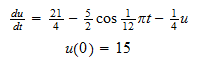Exact solution is:
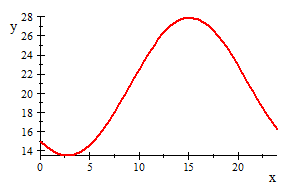
Next I find the Max temperature at
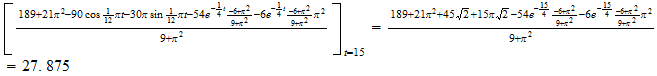
From the above calculating and
graph ,we can see that the temperature reaches its Max near
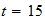;and
its Max temperature is about
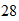
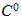
(b)solve the temperature in
June when the outside temperature is
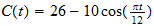and
the initial temperature is
,
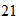
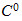
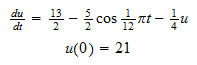Exact solution is:
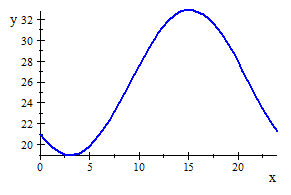
Next I find the Max temperature at
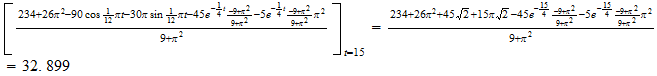
from the above calculate and the graph ,we can see that for the
June ,its Max temperature is about
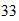
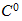
Again the Max temperature is also near
,and
its value is
conclusion:
From the above comparison ,we can see that during the month of
April and June in Atlanta,
Georgia, the outside Max temperature time is around
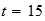;in
other words ,around
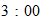pm
,it is hottest; Advice you not to go out at the time;
so we can get that first_order linear differential equations can be used to
solve a variety of problems that involve temperature ;We can use the basic
principle NEWTON'S LAW OF COOLING to find the
temperature of the body ,solving some complex practical problems;
.It is likely that many of the future application that will best exploit the technological capability of temperature problem have yet to be developed;
Bibliography
Differential equations with maple
Author is Martha l.abell/james p.braselton
Class no. in library of NP: QA371.5 D37 A141