The movement of the pendulum and the swing

General problem description:

Once I saw a girl in a garden playing with the swing . Before she start to play , her father gave a certain velocity to the swing.And the swing started moving on and on and finally it stopped . If we know the numerical values of initial velocity and mass of the the girl and the swing, we can find out the movement of the swing with respect to time. The movement of the pendulum came into my mind.But the pendulum of a clock seems never stop.

The movement of the pendulum and that of the swing are pretty similar and we can find out their displacemets with respect to time by using differential equation.

To find the movement of the pendulum

Problem description:

We find out that when the pendulum is in the vertical position , the maximum point where the

pendulum can reach is metre and the constant is found out to be

From there we can get the necessary information to solve the problem.

A simple harmonic equation can be described as

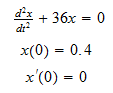, Exact solution is:

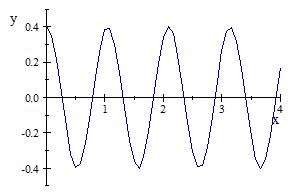The movement of the pendulum

To find the movement of thd swing

Problem description:

The weight of the girl and the swing is . And the initial velocity is And the air resistance is times of the velocity and frictional loss constant is The movement started from of the original position .(All the values are assumed approximately)

Solution:

we can set the equation by using Newton's Law of motion which states that the external force applied is equal to the product of the mass and the acceleration.

where is

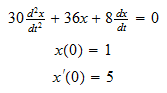, Exact solution is:

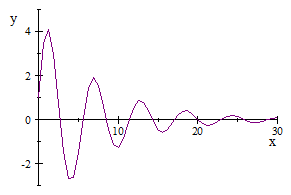The movemet of the swing

Conclusion:

For the pendulum case, it is moving continuously and it seems never stop.After solving the equation we find out that its movement is like a cosine waveform and it is oscillating.

In the case of the swing , the swing start moving and it speed become slower and slower and finally it stops.And the waveform is

It means that the sum of sine wave and cosine wave decrease exponentially.

We find this kind of problems in our daily life . If we have a better understanding in how to solve differential equations using the steps used above,and it is a marvel of life.

Bibliography

1) Basic Technical mathematics with calculus by Allan J Washinton

2) www. drmath.com

3) Engineering Sciences Text books