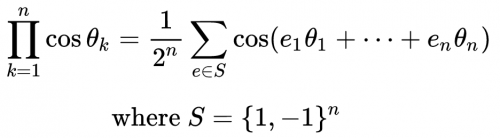IntMath forum | General
Explain notation for sum of cos terms [Solved!]
gtr109 02 Apr 2018, 22:34
My question
Please explain the meaning of the notation used in Wikipedia for a trig identity involving the product and sum of cosines where more than two angles are involved. What does the expanded identity look like for the number of angles equals, say, four or five? I have tried substituting for n equals two or three but do not understand the notation. I am attaching an image of the identity copied from Wikipedia.
Thank you.
Relevant page
Product to Sum Trigonometric Identities
What I've done so far
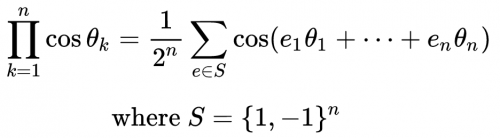
X
Please explain the meaning of the notation used in Wikipedia for a trig identity involving the product and sum of cosines where more than two angles are involved. What does the expanded identity look like for the number of angles equals, say, four or five? I have tried substituting for n equals two or three but do not understand the notation. I am attaching an image of the identity copied from Wikipedia.
Thank you.
Relevant page
<a href="https://en.wikipedia.org/wiki/List_of_trigonometric_identities#Product-to-sum_and_sum-to-product_identities">Product to Sum Trigonometric Identities</a>
What I've done so far
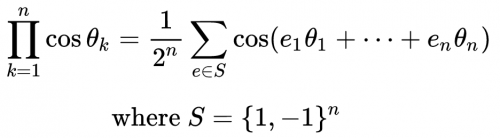
Re: Explain notation for sum of cos terms
Murray 06 Apr 2018, 03:51
@gtr109 OK, let's start with the left hand side of the equation.
Can you expand out the first 4 terms, that is `prod(k=1)^4 cos thetak`?
BTW - this is the formula from Wikipedia entered using the IntMath Forum's math entry system:
`prod(k=1)^n cos thetak ` ` =1/2^n sum(e in S) cos(e1 theta1 + ... + en thetan)` where `S={1,-1}^n`
X
@gtr109 OK, let's start with the left hand side of the equation.
Can you expand out the first 4 terms, that is `prod(k=1)^4 cos thetak`?
BTW - this is the formula from Wikipedia entered using the IntMath Forum's math entry system:
`prod(k=1)^n cos thetak ` ` =1/2^n sum(e in S) cos(e1 theta1 + ... + en thetan)` where `S={1,-1}^n`Re: Explain notation for sum of cos terms
Murray 20 Dec 2018, 20:29
Seems like gtr109 has disappeared. Anyone else like to take this up?
X
Seems like gtr109 has disappeared. Anyone else like to take this up?
Re: Explain notation for sum of cos terms
stephenB 10 Jan 2019, 16:58
The first 4 terms of `prod(k=1)^4 cos thetak` are:
`cos theta1 + cos theta2 + cos theta3 + cos theta4`
Right?
X
The first 4 terms of `prod(k=1)^4 cos thetak` are:
`cos theta1 + cos theta2 + cos theta3 + cos theta4`
Right?
Re: Explain notation for sum of cos terms
Murray 10 Jan 2019, 17:31
@stephenB: Are you maybe confusing product notation with summation notation?
X
@stephenB: Are you maybe confusing product notation with summation notation?
Re: Explain notation for sum of cos terms
stephenB 10 Jan 2019, 17:33
Oh yah. Should it be:
`cos theta1 * cos theta2 * cos theta3 * cos theta4`?
X
Oh yah. Should it be:
`cos theta1 * cos theta2 * cos theta3 * cos theta4`?
Re: Explain notation for sum of cos terms
Murray 10 Jan 2019, 17:37
@stephenB: Yes, that looks more like it, except (just to be picky), we either say:
"the first 4 terms of `prod(k=1)^n cos thetak ` are ..."
(it's a general statement, with variable `n` at the top of the summation), or we would write it as an equality (with the "4" at the top of the summation sign):
`prod(k=1)^4 cos thetak` `=cos theta1 * cos theta2 * cos theta3 * cos theta4`
Now, how about that right hand side - can you write out the first 4 terms of ` 1/2^n sum(e in S) cos(e1 theta1 + ... + en thetan)` where `S={1,-1}^n`?
X
@stephenB: Yes, that looks more like it, except (just to be picky), we either say:
"the first 4 terms of `prod(k=1)^n cos thetak ` are ..."
(it's a general statement, with variable `n` at the top of the summation), or we would write it as an equality (with the "4" at the top of the summation sign):
`prod(k=1)^4 cos thetak` `=cos theta1 * cos theta2 * cos theta3 * cos theta4`
Now, how about that right hand side - can you write out the first 4 terms of ` 1/2^n sum(e in S) cos(e1 theta1 + ... + en thetan)` where `S={1,-1}^n`?Re: Explain notation for sum of cos terms
stephenB 10 Jan 2019, 22:18
I had no idea what `S={1,-1}^n` meant and after some digging I found:
"If n is a natural number and A is an arbitrary set, the expression An is often used to denote the set of ordered n-tuples of elements of A. This is equivalent to letting An denote the set of functions from the set {0, 1, 2, ..., n-1} to the set A; the n-tuple (a0, a1, a2, ..., an-1) represents the function that sends i to ai." [Source: Exponentiation]
Then I needed to figure out what an "n-tuple" was. I gather from Wikipedia's Tuple article that it's like an ordered set, where the order matters.
But I'm stuck there. I don't know how to relate that to that last expression given.
X
I had no idea what `S={1,-1}^n` meant and after some digging I found:
"If n is a natural number and A is an arbitrary set, the expression A<sup>n</sup> is often used to denote the set of ordered n-tuples of elements of A. This is equivalent to letting A<sup>n</sup> denote the set of functions from the set {0, 1, 2, ..., n-1} to the set A; the n-tuple (a0, a1, a2, ..., an-1) represents the function that sends i to ai." [Source: <a href="https://en.wikipedia.org/wiki/Exponentiation#Oversets">Exponentiation</a>]
Then I needed to figure out what an "n-tuple" was. I gather from <a href="https://en.wikipedia.org/wiki/Tuple">Wikipedia's Tuple article</a> that it's like an ordered set, where the order matters.
But I'm stuck there. I don't know how to relate that to that last expression given.Re: Explain notation for sum of cos terms
Murray 11 Jan 2019, 01:54
OK, good
One of the best ways to figure out such formulas is to substitute real numbers in and see what's going on.
Let's start with `n=2` to keep it simple.
A "tuple" is like an ordered set, where the order of the numbers matters, and we need to choose all possible combinations of those numbers.
So in this case, `S={1,-1}^2` means "choose all the combinations of `1` and `-1`, two at a time. We obtain:
`S = {{1,1}, {-1,-1}, {-1,1}, {1,-1}}`
For the expression inside the cosine on the right, we need to multiply the angles (`theta`s) by those combinations.
Let's choose the (random, for illustration) angles `theta1=3` and `theta2=4` (these are in radians, of course).
So the summation expression on the right becomes for this example:
`1/2^2(cos(3+4)+cos(-3-4)+cos(-3+4)+cos(3-4))`
`=1/4(cos(7)+cos(-7)+cos(1)+cos(-1))`
Now, since cosine is an even function (that is `cos(-t)=cos(t)`), we can write:
`=1/4(2cos(7)+2cos(1))`
`=1/2(cos(7)+cos(1))`
So we are claiming:
`cos(3)cos(4) =1/2(cos(7)+cos(1))`
Is it correct?
There is a well-known trigonometric identity:
`cos(A)cos(B)=1/2 (cos(A+B)+cos(A-B))`
Our answer fits with this identity. (We could also just check it by calculator. Both sides give `0.6471`.)
Now, do you think you can extend this to the `n=3` case?
X
OK, good
One of the best ways to figure out such formulas is to substitute real numbers in and see what's going on.
Let's start with `n=2` to keep it simple.
A "tuple" is like an ordered set, where the order of the numbers matters, and we need to choose all possible combinations of those numbers.
So in this case, `S={1,-1}^2` means "choose all the combinations of `1` and `-1`, two at a time. We obtain:
`S = {{1,1}, {-1,-1}, {-1,1}, {1,-1}}`
For the expression inside the cosine on the right, we need to multiply the angles (`theta`s) by those combinations.
Let's choose the (random, for illustration) angles `theta1=3` and `theta2=4` (these are in radians, of course).
So the summation expression on the right becomes for this example:
`1/2^2(cos(3+4)+cos(-3-4)+cos(-3+4)+cos(3-4))`
`=1/4(cos(7)+cos(-7)+cos(1)+cos(-1))`
Now, since cosine is an even function (that is `cos(-t)=cos(t)`), we can write:
`=1/4(2cos(7)+2cos(1))`
`=1/2(cos(7)+cos(1))`
So we are claiming:
`cos(3)cos(4) =1/2(cos(7)+cos(1))`
Is it correct?
There is a well-known trigonometric identity:
`cos(A)cos(B)=1/2 (cos(A+B)+cos(A-B))`
Our answer fits with this identity. (We could also just check it by calculator. Both sides give `0.6471`.)
Now, do you think you can extend this to the `n=3` case?Re: Explain notation for sum of cos terms
stephenB 06 Jan 2020, 02:03
For `n=3`, we'd have for the left side (with `theta1=3`, `theta2=4` and `theta3=5`)
`prod(k=1)^3 cos thetak` `=cos 3 * cos 4 * cos 5`
The right side would be:
`1/2^3 (cos(3+4+5)+cos(-3-4-5)` `+cos(-3+4+5)` `+cos(3-4+5)` `+cos(-3+4-5)` `+cos(3+4-5)` `{:+cos(-3-4+5)` `{:+cos(3-4-5))`
`=1/8(cos(12)+cos(-12)+cos(6)` `+cos(4)` `+cos(-4)` `+cos(2)` `+cos(-2)` `{:+cos(-6))`
`=1/4(cos(12)+cos(6)+cos(4)+cos(2))`
Both left and right side `~~0.183558`, so it appears to work.
X
For `n=3`, we'd have for the left side (with `theta1=3`, `theta2=4` and `theta3=5`)
`prod(k=1)^3 cos thetak` `=cos 3 * cos 4 * cos 5`
The right side would be:
`1/2^3 (cos(3+4+5)+cos(-3-4-5)` `+cos(-3+4+5)` `+cos(3-4+5)` `+cos(-3+4-5)` `+cos(3+4-5)` `{:+cos(-3-4+5)` `{:+cos(3-4-5))`
`=1/8(cos(12)+cos(-12)+cos(6)` `+cos(4)` `+cos(-4)` `+cos(2)` `+cos(-2)` `{:+cos(-6))`
`=1/4(cos(12)+cos(6)+cos(4)+cos(2))`
Both left and right side `~~0.183558`, so it appears to work.Re: Explain notation for sum of cos terms
Murray 06 Jan 2020, 02:34
@stephenB: Well done!
@gtr109: I hope that helps you to understand how that notation works.
X
@stephenB: Well done!
@gtr109: I hope that helps you to understand how that notation works.
Related General questions
 Welcome to the IntMath Forum!
Welcome to the IntMath Forum!
The aim in the IntMath Forum is to help you to figure out how to... Murray 23 Nov 2015, 02:03 IntMath Forum Principles
IntMath Forum Principles
The IntMath Forum follows 5 simple principles to make it useful and enjoyable for all.
1.... Murray 25 Jan 2016, 02:41- Inequalities graph [Pending...]
hi. i met a problem while studying. could u help me solve?
sketch a region A... brucecy92 25 Jul 2020, 06:58
- Your site is a great help
Frankly speaking,You did a very wonderful job because IntMath has been a great help. keep... Christian 24 Dec 2015, 09:48
- Well Done! [Solved!]
I wants to use this opportunity thanking you for the job welldone.coz it has enlighten... Jephthah 18 Dec 2015, 10:28
top