3-D Earth Geometry
An interesting topic in 3-dimensional geometry is Earth geometry. The Earth is very close to a sphere (ball) shape, with an average radius of `6371\ "km"`. (It's actually a bit flat at the poles, but only by a small amount).
Earth geometry is a special case of spherical geometry. When we measure distances that a boat or aircraft travels between any 2 places on the Earth, we do not use straight line distances, since we need to go around the curve of the Earth from one place to another. (Think about the direct or straight-line distance between London and Sydney, through the Earth. That's going to be a lot less than the distance a plane flies around the surface of the Earth.)
Let's start with an example. What distance does a plane fly between Beijing, China and Perth, Western Australia?
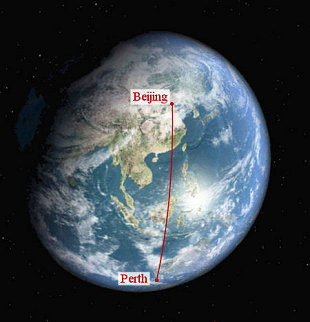
To figure this out, we need to understand latitude and longitude first.
Latitude and Longitude
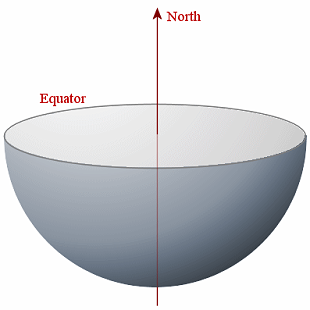
First, we represent the Earth by a sphere:

We slice the Earth through the equator and remove the top. We show the Earth's axis which (by convention) points to North at the top.
Parallels of Latitude
We want to be able to indicate how far North or South of the equator we are for any point on the Earth's surface.
For example, we wish to connect all the points that are 30o N of the equator. We do that by drawing a line from the centre of the Earth to the surface of the Earth, 30o up from the horizontal. We then draw a circle around the Earth parallel to the equator through the point where the 30o line meets the surface of the Earth. We can do the same thing for below the equator, in a southerly direction.
The angle from the horizontal through the equator determines the name given to each parallel of latitude. Five parallels of latitude are shown in the diagram; 60o N, 30o N, 0o N (the equator), 30o S and 60o S.
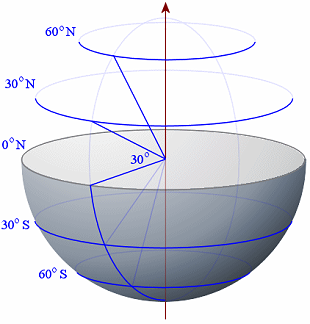
Each 1o of latitude on the Earth represents 60 nautical miles, or around 110.9 km.
Of course, 90o N represents the North pole and 90o S is the south pole.
Parallels of latitude give an indication of where a place (or a boat or a plane) are positioned in a northerly or southerly direction from 0o N (the equator).
Calculating the central angle for Beijing-Perth
Since `sin theta = 3738.11/6371` and the central angle is twice θ, we have:
Central angle = `2arcsin(3738.11/6371)` `= 2 xx 0.6270249` `= 1.254049`
(Radians, of course, and full calculator accuracy was used throughout, but not shown.)
Now, to find the distance travelled, we need to use our formula for arc length that we learned before (see Arc Length). If r is the radius of the great circle and θ is the angle subtended at the centre (in radians), the arc length s is given by:
s = rθ
Now, the average radius of the Earth is `6371\ "km"`, and the angle we just found is `1.254049` radians, so the flying distance from Beijing to Perth is given by:
s = 6371 × 1.254049 = 7989 km.
[Thanks to reader Paul Holland for the above suggested procedure.]
b. Haversine's Formula
Haversine's formula for the central angle of a sphere is more direct than the procedure we used above. It is given by (angles in radians):
Central angle = `2\ arcsin sqrt( sin^2 ((varphi_2-varphi_1)/2) +cos\ varphi_1\ cos\ varphi_2\ sin^2 ((lambda_2-lambda_1)/2) )`
where
φ1 and φ2 are the latitudes of the first and second place respectively (we used P1 and P2 before); and
λ1 and λ2 are the longitude of the first and second place respectively (we used Q1 and Q2 before);
(See Haversine Formula for a derivation of the above formula.)
Using our results from above, we have:
Beijing: φ1 = 39o54' N = 0.696386; λ1 = 116o24' E = 2.031563.
Perth: φ2 = 31o57' S = −0.557633; λ2 = 115o52' E = 2.022255.
Applying the Haversine formula gives us:
Central angle =
`2 arcsin sqrt( sin^2 ((-1.254)/2) +cos (0.696) cos (-0.557) sin^2 ((-0.009)/2) )`
= 1.254049
(radians once again, and full calculator accuracy was used throughout, but not shown)
Once again, using the arc length formula
s = rθ,
we one again obtain:
s = 6371 × 1.254049 = 7989 km.
Exercises
1. Find the shortest distance that an aircraft flies from Athens (38o N, 24o E) to Hong Kong (22o N, 114o E).
Answer
Expressing latitude and longitude in radians:
Athens: P1 = 38o N = 0.6632251;
Q1 = 24o E = 0.418879.
Hong Kong: P2 = 22o N = 0.3839724;
Q2 = 114o E = 1.989675
We now find the x-, y-, and z-coordinates for Athens and Hong Kong, given that the radius of the Earth is 6371 km:
Athens
x1 = 6371 cos 0.6632 cos 0.4189 = 4586.4
y1 = 6371 cos 0.6632 sin 0.4189 = 2042.1
z1 = 6371 sin 0.6632 = 3922.3
Hong Kong
x2 = 6371 cos 0.3840 cos 1.9897 = -2402.7
y2 = 6371 cos 0.3840 sin 1.9897 = 5396.3
z2 = 6371 sin 0.3840 = 2386.8
Now for the straight line distance between the 2 cities (directly, through the Earth), using the 3-D distance formula:
`sqrt ((-2402.7- 4586.4)^2+ (5396.3-2042.1)^2+ (2386.8-3922.3)^2)` `= 7902.9" km"`
Next, we find the central angle.
`7902.9/2=3851.5`,
and since `sin theta = 3851.5/6371` and the central angle is twice θ, we have:
Central angle = `2arcsin(3851.5/6371)` `= 2 xx 0.64918 ` `= 1.29836`
(Radians, of course, and full calculator accuracy was used throughout, but not shown.)
We use
s = rθ
giving
s = 6371 × 1.29836 = 8272 km.
[Thanks to reader Paul Holland for the above example.]
2. Find the distance that an aircraft must fly from London to Los Angeles if it flies directly, using Haversine's Formula.
Answer
"If it flies directly" means that it will fly a great circle route.
Here's the route (London is near the bottom of the image, Los Angeles near the top):
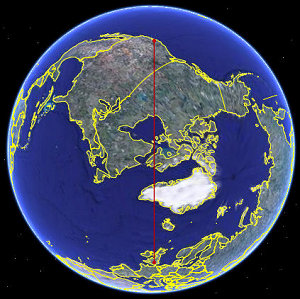
Image from Google Earth.
We learned above that the latitude and longitude for London and Los Angeles are as follows:
London: φ1 = 51o 32' N = 0.899426,
λ1 = 0o 5' W = −0.001454
Los Angeles: φ2 = 34o 3' N = 0.594285,
λ2 = 118o 14' W = −2.063561
Applying the formula for the central angle gives:
Central angle =
`2 arcsin sqrt( sin^2 ((-0.305)/2) +cos (0.899) cos (0.594) sin^2 ((-2.062)/2) )`
= 1.374296 (full calculator accuracy was used throughout)
So the distance between London and Los Angeles is:
s = rθ = 6371 × 1.374296 = 8756 km
