9. Integration Using Tables of Integrals
by M. Bourne
Leibniz's original integral notation
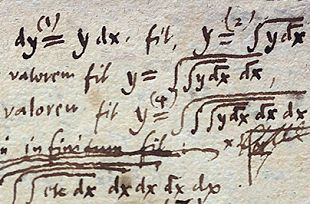
Gottfried Leibniz's original notation for integrals included an overbar, similar to what we use with square roots today. [Image source]
A lot of the integrals in this section can easily be done using a Table of Integrals. (Of course, use a computer to do integrals whenever you can!)
Points to note:
- It's very important to understand the substitutions `u` and `du` (which is the case for most integrations)
- Make sure you use the correct formula!! Some are very similar to others.
- Even if you are supplied with a table of integrals in examinations, learn as many as you can, and especially learn the conditions that apply. Too many students try to find the right one in the table, but have no idea what they are doing!
See: Table of Common Integrals
Example using Table of Integrals
Find the following integral, using table of integrals:
`inte^(2x)\ sin 3x\ dx`
Answer
We recognize this is the required formula:
`inte^(au)\ sin bu\ du` `=(e^(au)(a\ sin bu-b\ cos bu))/(a^2+b^2)+K`
For this example, we use:
`a = 2`
`b = 3`
`u = x`
So
`inte^(2x)sin 3x\ dx=(e^(2x)(2\ sin 3x-3\ cos 3x))/(2^2+3^2)+K`
`=(e^(2x)(2\ sin 3x-3\ cos 3x))/13+K`
There are some more examples of using the Table of Integrals in the section, Integration by Reduction Formulae.
