5. Integration: Other Trigonometric Forms
by M. Bourne
We can use the trigonometric identities that we learned earlier to simplify the integration process.
The main identities are shown here for reference:
`cos^2x+sin^2x=1`
`1+tan^2x=sec^2x`
`1+cot^2x=csc^2x`
`2\ cos^2x=1+cos 2x`
`2\ sin^2x=1-cos 2x`
The process that we use involves using the trigonometric ratios to simplify the expression, or to get the expression into a form that can be integrated.
Integrating a Product of Powers of Sine and Cosine - one power odd
To integrate a product of powers of sine and cosine, we use
`cos^2x+sin^2x=1`
if at least one of the powers is odd.
Example 1
Integrate: `int3\ cos^3x\ dx`.
Answer
`int3\ cos^3x\ dx`
`=3int(cos^2x)cos x\ dx`
`=3int(1-sin^2x)cos x\ dx`
`=3int(cos x\ -sin^2x\ cos x\) dx`
Letting `u=sin x`, and thus `du=cos x\ dx` gives:
`=3[sin x+K_1-intu^2du]`
`=3[sin x-(u^3)/3+K]`
`=3[sin x-(sin^3x)/3+K]`
Integrating a Product of Powers of Sine and Cosine - powers even
We use
`2\ cos^2x=1+cos 2x`
or
`2\ sin^2x=1-cos 2x`
if the power of `sin x` or `cos x` is even.
Example 2
Integrate: `intcos^2\ 2x\ dx`.
Answer
`intcos^2 2x\ dx`
Let `u=2x`, then `du=2\ dx`
This gives:
`intcos^2u(du)/2 =1/2intcos^2 u\ du`
`=1/2int(1+cos 2u)/2du`
`=1/4int1+cos 2u\ du`
`=1/4[u+(sin 2u)/2]+K`
`=1/4[2x+(sin 2(2x))/2]+K`
`=x/2+(sin 4x)/8+K`
Example 3
Integrate: `6intcot^3x\ dx`.
Answer
We have:
`6intcot^3x\ dx =6int(cot^2 x)cot x\ dx`
`=6int(csc^2x-1)cot x\ dx`
`=6(intcsc^2 x\ cot x\ dx` `{:-intcot x\ dx)`
Take the `intcsc^2x\ cot x\ dx` integral first:
Let `u = cot x`, then `du = -csc^2x\ dx`
So
`intcsc^2x\ cot x\ dx =-intu\ du`
`=-u^2/2+C`
`=-(cot^2x)/2+C`
For the second integral, from our table, we have
`intcot x\ dx=ln\ |sin x|+C`
Returning to the main question:
`6intcot^3x\ dx =6(intcsc^2x\ cot x\ dx-` `{:intcot x\ dx)`
`=6(-(cot^2x)/2-ln\ |sin x|)+K`
`=-3\ cot^2x-6\ ln\ |sin x|+K`
Application - Root Mean Square Value
The root mean square value of the function y with respect to x is given by:
`y_("rms")=sqrt(1/T int_0^T y^2dx`
where T is the period of y.
(See Period of Sine and Cosine if you are not sure about this.)
Effective Current
A common use of this concept is effective current. This is the value of the direct current that would produce the same quantity of heat energy in the same time as a certain alternating current. It is used in the design of heaters.
Example 4
Find the root mean square (rms) value of i = 3 + 2 cos t.
Answer
In this case, T = 2π.
So
`i_("rms") =sqrt(1/Tint_0^Ti^2dt)`
`=sqrt(1/(2pi)int_0^(2pi)(3+2\ cos t)^2dt)`
Now
`(3+2\ cos t)^2=9+12\ cos t+4\ cos^2 t`
Since `cos 2t = 2 cos^2 t - 1`, it follows that `cos^2t=(cos 2t+1)/2`.
So
`(3+2\ cos t)^2 =9+12 cos t+4((cos 2t+1)/2)`
`=9+12 cos t+2(cos 2t+1)`
`=11+12\ cos t+2\ cos 2t`
So
`int_0^Ti^2dt =int_0^(2pi)(11+12\ cos t+2\ cos 2t)dt`
`=[11t+12\ sin t+sin 2t]_0^(2pi)`
`=22pi`
And, finally:
`i_("rms") =sqrt(1/Tint_0^Ti^2dt) `
`=sqrt((22pi)/(2pi))`
`=sqrt11`
`=3.317`
This is a graph of our cosine current with the RMS effective current shown.
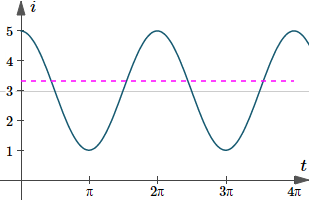
Graph of `i(t)=3+2cos(t)`, with the RMS current indicated by the dashed magenta line.
Example 5
For a current i given by i = i0 sin ωt, show that the root-mean-square of the current for one period is `(i_0)/sqrt2.`
Answer
In this case,
`T=(2pi)/omega`
So
`i_("rms")=sqrt(1/T int_0^Ti^2dt)`
`=sqrt(omega/(2pi)int_0^((2pi)/omega)(i_0\ sin omegat)^2dt)`
`=sqrt((omega(i _0)^2)/(2pi)int_0^((2pi)/omega)sin^2omegat\ dt)`
Let's just take the integral part first, and put
`sin^2omegat=(1-cos 2 omegat)/2`
`int_0^(2pi//omega)sin^2omegat\ dt =1/2int_0^(2pi//omega)(1-cos 2 omegat)dt`
`=1/2[t-(sin 2omega t)/(2omega)]_0^(2pi//omega)`
`=1/2[((2pi)/omega-0)-(0-0)]`
`=pi/omega`
So
`i_("rms")=sqrt((omega(i_0)^2)/(2pi)int_0^((2pi)/omega)sin^2omegat\ dt)`
`=sqrt{(omega (i_0)^2)/(2pi)pi/omega}`
`=sqrt(((i_0)^2)/2)`
`=(i_0)/sqrt2`
This is what the question required us to show.
Exercises
Integrate each of the given functions:
1. `int_(pi//3)^(pi//2)sqrt(cos x)\ sin^3x\ dx`
Answer
`int_(pi//3)^(pi//2)sqrt(cos x)\ sin^3x\ dx`
Write `sin^3x ` `= sin^2x\ sin x` ` = (1 - cos^2x)(sin x)`
So, taking the indefinite case first:
`sqrt(cos x) sin^3x`
`=cos^(1//2)x(1-cos^2x)(sin x)`
`=(cos^(1//2)x-cos^(5//2)x)(sin x)`
Put `u = cos x` then `du = -sin x\ dx`
So
`intsqrt(cos x)\ sin^3x\ dx =int(cos^(1//2)x-cos^(5//2)x)(sin x)dx`
`=-int(u^(1//2)-u^(5//2))du`
`=-(2u^(3//2))/3+(2u^(7//2))/7+K`
`=-(2\ cos^(3//2) x)/3+(2\ cos^(7//2)x)/7+K`
So we have for the definite case:
`int_(pi//3)^(pi//2)sqrt(cos x)\ sin^3x\ dx =[-(2 cos^(3//2)x)/3+(2 cos^(7//2)x)/7]_(pi//3)^(pi//2)`
`=[(0+0)-(-0.23570+0.02525)]`
`=0.2104`
The solution for Exercise 1 represents the area under the curve `y(x)=sqrt(cos x)\ sin^3x\ dx` between `pi/3 <= x <= pi/2`. Here is that graph:
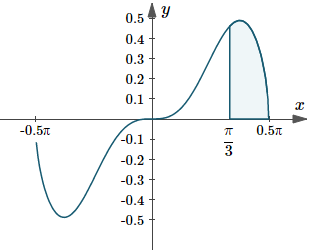
Graph of `y(x)=sqrt(cos x)\ sin^3x`, indicating the area under the curve from `x=pi/3` to `x=pi/2`.
Zooming out that graph shows it's periodic (it repeats itself) with period `2pi`. There are holes in the graph because of the `sqrt(cos x)` part (we can't have the square root of a negative number).
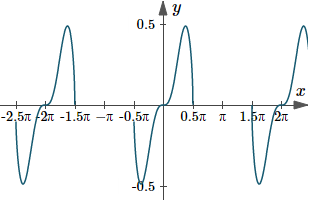
Graph of `y(x)=sqrt(cos x)\ sin^3x dx`, zoomed out to see its periodic nature.
2. `int_0^1sin^2 4x\ dx`
Answer
`int_0^1sin^2 4x\ dx`
We recall that
`2\ sin^2theta=1-cos 2theta`
In this case, if `θ = 4x`,
`2 sin^2 4x` `=1-cos [2(4x)]` `=1-cos 8x`
So `sin^2 4x=(1-cos 8x)/2`
`int_0^1sin^2 4x dx =1/2int_0^1(1-cos 8x) dx`
`=1/2[x-(sin 8x)/8]_0^1`
`=1/2[(1-0.9894/8)-(0-0)]`
`=0.4382`
Here is the graph of the integration we just found, indicating the area under the curve `y=sin^2 4x`.
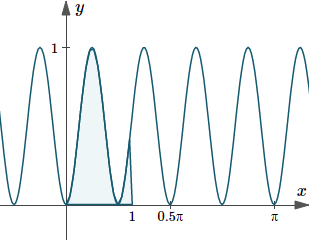
Graph of `y(x)=sin^2 4x`, indicating the area under the curve from `x=0` to `x=1`.
3. `intcot 4x\ csc^4 4x\ dx`
Answer
`int cot 4x\ csc^4 4x\ dx`
We write the expression under the integral sign as follows:
`cot 4x\ csc^4 4x\ dx` `=(csc^3 4x)\ cot 4x\ csc\ 4x`
Then, let `u = csc\ 4x` and so we have `du = -4\ csc\ 4x\ cot 4x\ dx`
That is, `-(du)/4 = csc\ 4x\ cot 4x\ dx`
Now we can perform the integral:
`int cot 4x\ csc^4 4x\ dx =int(csc^3 4x)\ cot 4x\ csc\ 4x\ dx`
`=-1/4intu^3du`
`=-u^4/16+K`
`=-(csc^4 4x)/16+K`
4. `intsqrt(tan x)\ sec^4x\ dx`
Answer
Recall that
`sec^2x=1+tan^2x`
So we can write the part under the integral as:
`sqrt(tan x)\ sec^4 x =(tan^(1//2) x)\ sec^2 x\ sec^2 x`
`=(tan^(1//2) x )(1+tan^2 x )sec^2 x`
`=(tan^(1//2) x+tan^(5//2)x)sec^2 x`
Next, we put `u = tan x`, giving `du = sec^2x\ dx`
So our integral becomes:
`int (tan^(1//2) x+tan^(5//2)x)sec^2 x\ dx =int(u^(1//2)+u^(5//2))du`
`=2/3u^(3//2)+2/7u^(7//2)+K`
`=2/3tan^(3//2)x+2/7tan^(7//2)x+K`
5. `int_(pi//6)^(pi//3)(2dx)/(1+sin x`
Answer
`int_(pi//6)^(pi//3)(2\ dx)/(1+sin x)`
We need to re-express this and we make use of a fairly common technique. We multiply the numerator (top) and denominator (bottom) of the fraction by the conjugate of the denominator. (The conjugate has the opposite sign in the middle. In this case, it's a minus sign.)
We will make use of this important result:
`sin^2 x+ cos^2 x = 1`
`1/(1+sin x) =1/(1+sin x)xx(1-sin x)/(1-sin x)`
`=(1-sin x)/(1-sin^2x)`
`=(1-sin x)/(cos^2 x)`
`=sec^2x-(sin x)/(cos^2 x)`
Now we can integrate.
Putting `u = cos x` in the right hand part, we have:
`du = -sin x\ dx`
So
`int_(pi//6)^(pi//3)(2\ dx)/(1+sin x)`
`=2int_(pi//6)^(pi//3)(sec^2x-(sin x)/(cos^2x))dx`
`=2[tan x-1/(cos x)]_(pi//6)^(pi//3)`
`=2[(1.73215-2)-` `{:(0.57735-1.15470)]`
`=0.6190`
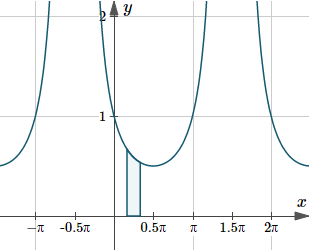
Graph of `y(x)=2/(1+sin(x))`, indicating the area under the curve from `x=pi/6` to `x=pi/3`.
Application - Length of a Curve
The length s of the arc of a curve y = f(x) from x = a to x = b is given by:
`s=int_a^bsqrt(1+((dy)/dx)^2dx`
Find the length of the curve y = ln (cos x) from `x=0` to `x=pi/3`.
Answer
The curve in this problem is `y = ln cos x`.
We need its derivative:
`(dy)/(dx)=-(sin x)/(cos x)=-tan x`
For this problem, we'll make use of an earlier result,
`1+tan^2 x=sec^2 x`
Applying the formula gives:
`s=int_a^bsqrt(1+((dy)/dx)^2)dx`
`=int_0^(pi//3)sqrt(1+(-tan x)^2)dx`
`=int_0^(pi//3)sqrt(1+tan^2x) dx`
`=int_0^(pi//3)sqrt(sec^2x) dx`
`=int_0^(pi//3)sec x\ dx`
`=[ln\ |sec x+tan x|]_0^(pi//3)`
`=[ln\ |sec (pi/3)+tan (pi/3)|` `{:-|ln(1)+ln(0)|]`
`=1.317`
Here's the graph of the arc length we just found (in pink). I needed to take the absolute value of the `cos(x)` values, otherwise there would be gaps in the graph (whenever `cos(x)` was negative).
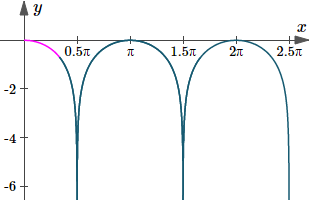
Graph of `y(x)=ln|cos x|`, with the curve length we just found indicated in magenta (pink).
