11. Integration by Partial Fractions
by M. Bourne
Partial fraction decomposition
![]()
Partial fraction decomposition - linear factors
If the integrand (the expression after the integral sign) is in the form of an algebraic fraction and the integral cannot be evaluated by simple methods, the fraction needs to be expressed in partial fractions before integration takes place.
The steps needed to decompose an algebraic fraction into its partial fractions results from a consideration of the reverse process − addition (or subtraction).
Consider the following addition of algebraic fractions:
`1/(x+2)+5/(x+3)=((x+3)+5(x+2))/((x+2)(x+3))`
`=(6x+13)/(x^2+5x+6)`
In this section, we want to go the other way around. That is, if we were to start with the expression
`(6x+13)/(x^2+5x+6)`
and try to find the fractions whose sum gives this result, then the two fractions obtained, i.e.
`1/(x+2)` and `5/(x+3)`,
are called the partial fractions of `(6x+13)/(x^2+5x+6)`.
We decompose fractions into partial fractions like this because:
- It makes certain integrals much easier to do, and
- It is used in the Laplace transform, which we meet later.
So if we needed to integrate this fraction, we could simplify our integral in the following way:
`int(6x+13)/(x^2+5x+6)dx` `=int1/(x+2)dx+int5/(x+3)dx`
We integrate the two fractions using what we learned in Basic Logarithmic Form:
`int(6x+13)/(x^2+5x+6)dx = int1/(x+2)dx+int5/(x+3)dx`
`=ln(x+2)+5\ ln(x+3)+K`
`=ln[(x+2)(x+3)^5]+K`
Here are the graphs of the original function, and the integral we just found.
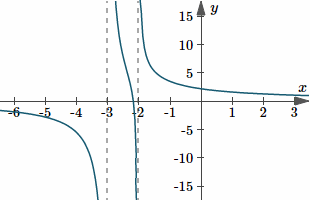
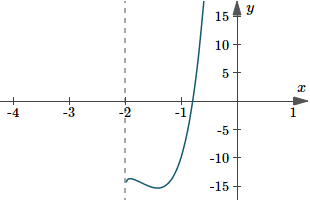
Graph of `y(x)=(6x+13)/(x^2+5x+6)`, and a typical integral solution `y(x)=ln(x+2)(x+3)^5+10` (where I've used `K=10`).
Next we'll see how to split such a fraction into its partial fractions.
Expressing a Fractional Function In Partial Fractions
RULE 1:
Before a fractional function can be expressed directly in partial fractions, the numerator must be of at least one degree less than the denominator.
Example 1
The fraction
`(2x^2+3)/(x^3-1)`
can be expressed in partial fractions whereas the fraction
`(2x^3+3)/(x^3-1)`
cannot be expressed directly in partial fractions.
However, by division
`(2x^3+3)/(x^3-1)` `=2+5/(x^3-1)`
and the resulting fraction can be expressed as a sum of partial fractions.
(Note: The denominator of the fraction must be factored before you can proceed.)
RULE 2: Denominator Containing Linear Factors
For each linear factor `(ax + b)` in the denominator of a rational fraction, there is a partial fraction of the form
`A/(ax+b)`
where `A` is a constant.
Example 2
Express the following in partial fractions. `(3x)/((2x+1)(x+4)`
Answer
We set:
`(3x)/((2x+1)(x+4))` ≡ `A/(2x+1)+B/(x+4)`
We find the values of `A` and `B` by multiplying both sides by `(2x + 1)(x + 4)`:
`3x = A(x + 4) + B(2x + 1)`
Then we expand and collect like terms:
`3x = (A + 2B)x + (4A + B)`
Next, we equate `x` and constant terms:
The `x` terms: gives `3 = A + 2B`
The constant terms gives: `0 = 4A + B`
Solving this set of simultaneous equations gives:
`A = -B/4`
`7B/4 = 3`
`B = 12/7`
`A = -3/7`
So `(3x)/((2x+1)(x+4))` `=(-3)/(7(2x+1))+12/(7(x+4))`
RULE 3: Denominator Containing Repeated Linear Factors
If a linear factor is repeated `n` times in the denominator, there will be `n` corresponding partial fractions with degree 1 to `n`.
For example, the partial fractions for
`(5x^3+7x-9)/((x+1)^4)`
will be of the form:
`(5x^3+7x-9)/((x+1)^4) ` `-= A/(x+1)+B/((x+1)^2)` `+C/((x+1)^3)` `+D/((x+1)^4)`
(The sign `-=` means "is identically equal to". We normally apply this between 2 expressions when we wish them to be equivalent. It's OK to use the ordinary equals sign, too.)
Example 3
(a) Express the following as a sum of partial fractions.
`(x+5)/((x+3)^2)`
Answer
`(x+5)/((x+3)^2)` `=A/(x+3)+B/((x+3)^2)`
Multiply both sides by `(x + 3)^2`:
`x + 5 = A(x + 3) + B`
Equating `x` parts and constant parts:
`1 = A``5 = 3A + B`
So `B = 2`.
So
`(x+5)/((x+3)^2)` `=1/(x+3)+2/((x+3)^2)`
Don't believe it is true! Add the right hand side and convince yourself about the accuracy of this process. You actually learn a lot about how it works by doing this. And it's always good to check your work!
(b) Express the following as a sum of partial fractions.
`(2x^2-3)/((x-1)^3(x+1))`
Answer
`(2x^2-3)/((x-1)^3(x+1))` `-=A/(x-1)` `+B/((x-1)^2)` `+C/((x-1)^3)` `+D/(x+1)`
We multiply throughout by `(x-1)^3(x+1)`:
`2x^2- 3` `= A(x - 1)^2(x + 1)` ` + B(x - 1)(x + 1)` ` + C(x + 1)` ` + D(x - 1)^3`
We do not need to expand all this out. Instead, we just use appropriate substitutions to find the values of the unknowns `A` to `D`.
Let `x = 1`:
LHS `=-1`
RHS `= 2C`
So `C = -1/2`
Let `x = -1`:
LHS `= -1`
RHS `= -8D`
So `D = 1/8`
We now compare the coefficients of `x^3` on both sides and then compare the constant values on both sides.
Coefficient of `x^3` on LHS `= 0`
Coefficient of `x^3` on RHS `= A + D`
So `A=-D`.
But since `D = 1/8`, we have `A = -1/8`.
Constant term on LHS `= -3`
Constant term on RHS `= A - B + C - D`
But since we know 3 values now, we have: `B = 9/4`.
So
`(2x^2-3)/((x-1)^3(x+1))` `=-1/(8(x-1))+9/(4(x-1)^2)` `-1/(2(x-1)^3)+1/(8(x+1)`
NOTE: Scientific Notebook can do all this directly for us using Polynomials/Partial Fractions.
RULE 4:Denominator Containing a Quadratic Factor
Corresponding to any quadratic factor `(ax^2+ bx + c)` in the denominator, there will be a partial fraction of the form
`(Ax+B)/(ax^2+bx+c)`
Example 4
Express the following in partial fractions.
`(x^3-2)/(x^4-1)`
Answer
Firstly, we need to factor the denominator. We just use difference of 2 squares, twice:
`x^4- 1 = (x^2+ 1)(x^2- 1)` ` = (x^2+ 1)(x + 1)(x - 1)`
So `(x^3-2)/(x^4-1)=(x^3-2)/((x^2+1)(x+1)(x-1)`
The partial fraction decomposition will be of the form:
`(x^3-2)/((x^2+1)(x+1)(x-1))` `=(Ax+B)/(x^2+1)+C/(x+1)+D/(x-1`
We multiply throughout by `(x^2 + 1)(x + 1)(x - 1)`:
`x^3 - 2 ` `-=(Ax + B)(x + 1)(x - 1)` ` + C(x^2 + 1)(x - 1)` ` + D(x^2 + 1)(x + 1)`
Let `x = 1`:
LHS `= -1`
RHS `= 4D`
So `D = -1/4`
Let `x = -1`:
LHS `= -3`
RHS `= -4C`
So `C = 3/4`
Coefficient of `x^3` on LHS `= 1`
Coefficient of `x^3` on RHS `= A + C + D`
Since `D = -1/4` and `C = 3/4`, then `A = 1/2`.
Constant term on LHS `= -2`
Constant term on RHS `= -B - C + D`
This gives us `B = 1`.
So
`(x^3-2)/((x^2+1)(x+1)(x-1))`
`=(1/2x+1)/(x^2+1)+3/(4(x+1))-1/(4(x-1))`
`=(x+2)/(2(x^2+1))+3/(4(x+1))-1/(4(x-1)`
Note: Repeated quadratic factors in the denominator are dealt with in a similar way to repeated linear factors.
Example:
`(x^2+1)/((x^2+x+1)^2)` `-=(Ax+B)/(x^2+x+1)+(Cx+D)/((x^2+x+1)^2`
Summary
| Denominator containing… | Expression | Form of Partial Fractions |
| a. Linear factor | `(f(x))/((x+a)(x+b))` | `A/(x+a)+B/(x+b)` |
| b. Repeated linear factors | `(f(x))/((x+a)^3)` | `A/(x+a)+B/((x+a)^2)+C/(x+a)^3` |
| c. Quadratic term
(which cannot be factored) |
`(f(x))/((ax^2+bx+c)(gx+h))` |
`(Ax+B)/(ax^2+bx+c)+C/(gx+h)` |
Note: In each of the above cases `f(x)` must be of less degree than the relevant denominator.
Exercises
Write the following fractions as sum of partial fractions and then integrate with respect to x.
1. `1/(x^2(x-2))`
Answer
`1/(x^2(x-2))` `=A/x+B/x^2+C/(x-2)`
We multiply both sides by `x^2(x-2)`:
`1 = Ax(x - 2) + B(x - 2) + Cx^2`
Let `x = 0`, and this gives `B = -1/2`.
Let `x = 2`, and this gives `C = 1/4`.
Comparing coefficients for `x^2`, we obtain `A + C = 0`.
So `A = -1/4`.
Therefore
`1/(x^2(x-2))`
`=A/x+B/x^2+C/(x-2)`
`=-1/(4x)-1/(2x^2)+1/(4(x-2))`
So the integral required is:
`int(dx)/(x^2(x-2))`
`=int(-1/(4x)-1/(2x^2)+1/(4(x-2)) )dx`
`=-1/4ln x+1/(2x)+1/4ln(x-2)+K`
2. `x^2/((2x+1)(x+2)^2`
Answer
`x^2/((2x+1)(x+2)^2)` `=A/(2x+1)+B/(x+2)+C/((x+2)^2)`
Multiplying both sides by `(2x+1)(x+2)^2` gives:
`x^2 = A(x + 2)^2 ` `+ B(2x + 1)(x + 2) ` `+ C(2x + 1)`Let `x = -2`, and this gives `C = -4/3`.
Let `x = -1/2`, and this gives `A = 1/9`.
Comparing coefficients of `x^2` gives: `A + 2B = 1`.
So `B = 4/9`.
Therefore
`x^2/((2x+1)(x+2)^2)` `=1/(9(2x+1))` `+4/(9(x+2))` `-4/(3(x+2)^2`
Now for the integration:
`int(x^2dx)/((2x+1)(x+2)^2)`
`=int(1/(9(2x+1))+4/(9(x+2))` `{:-4/(3(x+2)^2))dx`
`=1/18ln(2x+1)+4/9ln(x+2)` `{:+4/(3(x+2))+K`
