2. Functions from Verbal Statements
Example 1
When operating a factory, there are fixed costs like electricity, labor and storage space. One such factory has fixed costs of `$50,000` per day.
There are also variable costs, for example, if they make more widgets it will cost more in materials, extra labor costs and extra power costs. The factory calculates there is a variable cost of `$10` to manufacture each extra widget.
Write the daily cost C as a function of the number of units produced.
Answer
Let's say the factory produces x widgets per day. (We could choose any meaningful variable - n would also be a good choice.)
The daily total cost C equals the fixed cost of `$50,000` plus the variable cost of producing x units.
The cost of producing 1 unit is `$10`, so the cost of producing x units is `$10x`.
So the total cost C, where C is a function of x is
`C(x) = 50000 + 10x `
For example, the daily cost of making `2000` widgets is:
`C(2000)` ` = 50000 + 10 × 2000` ` = $70,000 `
Note that in this example, x can only take integer values of `0` or more (we can't make negative widgets).
The lowest cost is `$50,000` per day, when we make `0` widgets.
Example 2

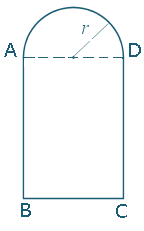
A Norman window has the shape of a rectangle with a semicircle on top, as shown.
Considering the space available, the base of each window has to be `30\ "cm"` less than the height of the rectangular part.
What is the perimeter p of the window as a function of the radius r of the circular part?
Answer
We label the points on the window for convenience:
Perimeter p is given by:
p = semicircle circumference + length AB + length BC + length CD
The circumference of a semi-circle is half the circumference of a circle:
`"curve"\ AD = 1/2(2pir) = pi r`
From the question, we know
AB = BC + 30
Also, we can see from the diagram
AD = BC = 2r
So, putting it all together, we have:
p = curve AD + AB + BC + CD
p = (πr) + (2r + 30) + 2r + (2r + 30)
Simplifying, we can write our function as
p = p(r) = π r + 6r + 60
Note the radius cannot be negative, and the window would not exist if `r = 0`.
Also, when we write "p = p(r)", we mean "p, which is a function of r".
Exercise
A Boeing 747 burns fuel at the rate of `13,000\ "kg/h"` while cruising. If the aircraft weighed `350,000\ "kg"` at take-off, express its weight w as a function of the time t, in hours.
Answer
The aircraft weighed 350,000 kg at takeoff and is losing weight as the flight goes on, so we need to subtract the fuel burn (in kg/h) multiplied by the time:
Answer: `w(t) = 350,000 - 13,000t`
For example, after flying for 6 hours, the aircraft would weigh:
`w(6) = 350,000 − 13,000 × 6` ` = 272,000\ "kg"`
Note: Like many mathematical models, this is a very simplified version of the real situation. A plane burns fuel at different rates during taxi (on the ground, where the engines run inefficiently), take-off (which is the time of maximum fuel burn), climb, cruise at the beginning (when it is heavy), cruise towards the end (when it is lighter), and descent (when it uses very little fuel).
Factoid: It costs upwards of US`$200,000` to fill the tanks of a 747.