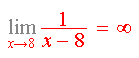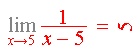1. Limits and Differentiation
by M. Bourne
On this page
Limit as x → some number
Limit as x → 0
Limit as x → ∞
Continuity & Differentiation
Split Functions & Differentiation
To understand what is really going on in differential calculus, we first need to have an understanding of limits.
Limits
In the study of calculus, we are interested in what happens to the value of a function as the independent variable gets very close to a particular value. We came across this concept in the Introduction, where we zoomed in on a curve to get an approximation for the slope of that curve.
Limits as x Approaches a Particular Number
Sometimes, finding the limiting value of an expression means simply substituting a number.
Example 1
Find the limit as t approaches `10` of the expression `P = 3t + 7`.
Answer
We write this using limit notation as: `lim_(trarr10)(3t+7)`
In this example there is no complication - we simply substitute and write
`lim_(trarr10)(3t+7)=37`
There is no complication because `f(t) = 3t + 7` is a continuous function.
But there are cases where we cannot simply substitute like this.
Example 2
We know that x cannot equal `3` in the following expression (because we cannot have a denominator equal to zero):
`f(x)=(x^2-2x-3)/(x-3)`
What is the value of the function as x approaches `3`?
Answer
We can see that the function approaches a particular value as x approaches `3` from the left:
| x | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 |
| f(x) | 3.5 | 3.6 | 3.7 | 3.8 | 3.9 |
Continuing, we get closer and closer to `x = 3`:
| x | 2.9 | 2.92 | 2.94 | 2.96 | 2.97 | 2.98 | 2.99 |
| f(x) | 3.9 | 3.92 | 3.94 | 3.96 | 3.97 | 3.98 | 3.99 |
Likewise, approaching `x = 3` from the right gives the same limit value:
| x | 3.5 | 3.1 | 3.01 | 3.00001 |
| f(x) | 4.5 | 4.1 | 4.01 | 4.00001 |
We note that the function value is getting closer and closer to `4`.
We write:
`lim_(xrarr3)(x^2-2x-3)/(x-3)=4`
NOTE: We could have evaluated this limit by factoring first:
`lim_(xrarr3)(x^2-2x-3)/(x-3)`
`=lim_(xrarr3)((x+1)(x-3))/(x-3)`
`=lim_(xrarr3)(x+1)`
`=4`
CAUTION: The factorising process is only possible in this example because we have: x ≠ 3.
This is a typical problem in the study of introductory limits. It appears to be a bit silly, in that we could have factored it, cancelled and substituted `x = 3` like we just saw. But the example is important for the concept that there is no actual value of the function when `x = 3`, but if we get really, really close to `3`, the function value is really close to some value (`4`, in this case).
Limits as x Approaches 0
We must remember that we cannot divide by zero - it is undefined.
But there are some interesting, and important, limits where there is a limiting value as x approaches `0` and where it would appear that we have a `0` denominator.
Example 3
Find the limit as x approaches `0` of `(sin\ x)/x`
Answer
Notice we cannot just substitute 0 because `(sin\ 0)/0` is undefined.
There is no algebraic process to find this limit. We can substitute values of x which get closer and closer to `0` (from both the left side and right side) and conclude that
`lim_(xrarr0)(sin\ x)/x=1.`
A way to check this is to graph it and see that indeed the limit as x gets closer to `0` is `1`:
We've indicated there is a "hole" at `x = 0` in our graph, using an open circle.
Limits as x Approaches Infinity
Example 4
Consider the fraction `5/x`. What happens as `x -> oo`?
Answer
Clearly, if we take larger and larger values of x, the value of the fraction becomes smaller and smaller until it gets very close to `0`. We say that "the limit of `5/x` as x approaches infinity is `0`".
We write this in mathematical notation as: `lim_(x->oo)(5/x)=0`.
Here is the graph of `y=5/x` (for positive `x`), showing the `y`-value gets closer to `0` as `x` increases:
Graph of `y=5/x`.
Limits when the variable is in the denominator
In general:
`lim_(x->+-oo)(1/(x))=0`
And similarly,
`lim_(x->+-oo)(1/(x^2))=0`
We use these limits when evaluating limits of functions and it is especially useful in curve sketching.
Example 5
Find the limit `lim_(x->oo)((5-3x)/(6x+1)).`
Answer
This time it is not so obvious what the limit value is. We could substitute larger and larger values of x until we could see what was happening (try `100`, then `1\ 000`, then `1\ 000\ 000` and so on).
Or, we could rearrange the expression and use the fact that
`lim_(x->oo)(1/x)=0`
to find the limiting value.
We divide throughout by x to get the expression in a form where we can evaluate it.
`lim_(x->oo)((5-3x)/(6x+1))`
`=lim_(x->oo)((5/x-3)/(6+1/x))`
`=(0-3)/(6+0)`
`=-1/2`
Notice that we cannot substitute ∞ into the fraction `((5/x-3)/(6+1))`, because this does not make mathematical sense.
Please do not write `((5-3(oo))/(6(oo)+1))`. It really upsets mathematicians.
Example 6
Find `lim_(x->oo)((1-x^2)/(8x^2+5))`
Answer
Numerical solution: We could substitute numbers which increase in size: `100`, then `10\ 000`, then `1\ 000\ 000`, etc and we would find that the value approaches `-1/8`.
Algebraic solution:
We first divide top and bottom of our fraction by `x^2`, then take limits.
`lim_(x->oo)((1-x^2)/(8x^2+5))`
`=lim_(x->oo)((1/x^2-x^2/x^2)/((8x^2)/(x^2)+5/x^2))`
`=lim_(x->oo)((1/x^2-1)/(8+5/x^2))`
`=-1/8`
Joke
After explaining to a student about limits, I gave him the following example:
I tried to check whether he really understood that, so I gave him a different example.
His answer was:
Continuity and Differentiation
In this chapter we will be differentiating polynomials. But later we will come across more complicated functions and at times, we cannot differentiate them. We need to understand the conditions under which a function can be differentiated.
Earlier we learned about Continuous and Discontinuous Functions.
A function like f(x) = x3 − 6x2 − x + 30 is continuous for all values of x, so it is differentiable for all values of x.
However, a function like `f(x)=2/(x^2-x)` is not defined for `x = 0` and `x = 1`.
It is discontinuous at those points. Hence, we cannot differentiate the function for those values.
Split Functions and Differentiation
We met Split Functions before in the Functions and Graphs chapter.
A split function is differentiable for all x if it is continuous for all x.
Example 7
We met this example in the earlier chapter.
`f(x)={(2x+3,text(for)\ x<1),(-x^2+2,text(for)\ x>=1):}`
This function has a discontinuity at x = 1, but it is actually defined for `x = 1` (and has value `1`). It is differentiable for all values of x except `x = 1`, since it is not continuous at `x = 1`.
Continuous functions
All of our functions in the earlier chapters on differentiation and integration will be continuous. In later chapters, we will see discontinuous functions, especially split functions. (see Fourier Series and Laplace Transforms)
Coming next...
We now move on to see how limits are applied to the problem of finding the rate of change of a function from first principles. This is the same as finding the slope of a tangent.