4. Applications: Derivatives of Trigonometric Functions
by M. Bourne
We can now use derivatives of trigonometric and inverse trigonometric functions to solve various types of problems.
Example 1
Find the equation of the normal to the curve of `y=tan^-1(x/2)` at `x=3`.
Answer
If you need a refresher, see the section on Tangent and Normals.
The derivative of `y=arctan(u)` is given by:
`(dy)/(du)=1/(1+(u)^2)`
In this example, we have `u=x/2`, so the derivative is:
`(dy)/(dx)=1/(1+(x/2)^2)(1/2)`
When `x = 3`, this expression is equal to: `0.153846`
So the slope of the tangent at `x = 3` is `0.153846`.
The slope of the normal at `x = 3` is given by:
`(-1)/0.153846=-6.5`
So the equation of the normal is given by:
(When `x = 3`, `y = 0.9828`)
`y − 0.9828 = -6.5(x − 3)`
That is,
`y = -6.5x + 20.483`
Here is the graph of our situation:
The graph of `y=arctan(x/2)` showing the tangent and the normal at `x=3.`
Example 2
The apparent power Pa of an electric circuit whose power is P and whose impedance phase angle is θ, is given by
`P_a = P sec θ`.
Given that P is constant at 12 W, find the time rate of change of Pa if θ is changing at the rate of 0.050 rad/min, when θ = 40°.
Answer
Using chain rule, we have:
`(dP_a)/(dt)=(dP_a)/(d theta)(d theta)/(dt)`
Now `P_a= P sec θ = 12 sec θ` (since `P = 12\ "W"`)
`(dP_a)/(d theta)=12 sec theta tan theta`
We are told
`(d theta)/(dt)=0.050`
So
`(dP_a)/(dt)=(dP_a)/(d theta)(d theta)/(dt)`
`=(12 sec theta tan theta)(0.050)`
`=0.6 sec theta tan theta`
When θ = 40°, this expression is equal to: 0.657 W/min.
Example 3
A machine is programmed to move an etching tool such that the position of the tool is given by x = 2 cos 3t and y = cos 2t, where the dimensions are in cm and time is in s. Find the velocity of the tool for t = 4.1 s.
Answer
`v_x=(dx)/(dt)=-6 sin 3t`
`v_y=(dy)/(dt)=-2 sin 2t`
At `t = 4.1`, `v_x = 1.579` and `v_y = -1.88`.
So
`v=sqrt((v_x)^2+(v_y)^2)`
`=sqrt((1.579)^2+(-1.88)^2)`
`=2.46\ "cm"//s`
For velocity, we need to also indicate direction. First, we find the appropriate acute angle (the "reference" angle):
`alpha=tan^-1(1.88 / 1.579)=50^@`
So since we are in the 4th quadrant when `v_x` is positive and `v_y` is negative, the required angle is `360^@ - 50^@ = 310^@`.
(See the following for background on how to find this angle: Trigonometric Functions of any Angle.)
Example 4
The television screen at a sports arena is vertical and 2.4 m high. The lower edge is 8.5 m above an observer's eye level. If the best view of the screen is obtained when the angle subtended by the screen at eye level is a maximum, how far from directly below the screen must the observer be?
Answer
(Diagam not to scale)
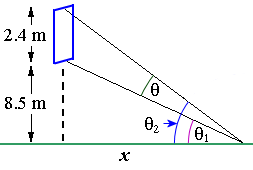
We define θ1 and θ2 as shown in the diagram such that:
`θ = θ_2 - θ_1`.
Let x be the distance from directly under the screen to the observer. To maximise `θ,` we will need to find
`dy/dx`
and then set it to 0.
We note that
`tan theta_1=8.5/x`, and
`tan theta_2=10.9/x`
This gives:
`theta_1=tan^-1(8.5)/x ` and
`theta_2=tan^(-1) 10.9/x`
Now since `θ = θ_2 - θ_1`,
`theta=tan^-1 10.9/x-tan^-1 8.5/x`
We have a function of a function in each term.
Now, in the first term, if we let
`u=10.9/x=10.9x^-1`
then
`(du)/(dx)=d/(dx)(10.9x^-1)`
`=-10.9x^-2`
`=-10.9/x^2`
Similarly for the second term, we will have:
`d/(dx)(8.5x^-1)`
`=-8.5x^-2`
`=-8.5/x^2`
So we have:
`(d theta)/(dx)=1/(1+((10.9)/x)^2)(-10.9/x^2)` `-1/(1+((8.5)/x)^2)(-8.5/x^2)`
`=1/x^2((-10.9)/(1+(10.9^2)/(x^2))+8.5/(1+(8.5^2)/(x^2)))`
Next, we multiply the x2 in the denominator (bottom) of the first fraction by the denominators of the 2 fractions in brackets, giving:
`=(-10.9)/(x^2+10.9^2)+8.5/(x^2+8.5^2)`
`=(-10.9(x^2+8.5^2)+8.5(x^2+10.9^2))/((x^2+10.9^2)(x^2+8.5^2))`
`=(-2.4x^2+222.36)/((x^2+10.9^2)(x^2+8.5^2))`
To find when this equals `0`, we need only determine when the numerator (the top) is `0`.
That is
`-2.4x^2 + 222.36 = 0`
This occurs when `x = 9.63` (we take positive case only)
So the observer must be `9.63\ "m"` from directly below the screen to get the best view.
Example 5
A winch on a loading dock is used to drag a container along the ground. The winch winds the cable in at 2ms-1 and is 5 m above the ground. At what rate is the angle θ between the cable and the ground changing when 10 m of cable is out?
Answer
Scalar Diagram (involving distances only):
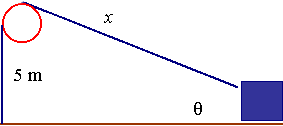
We can see that:
`sin theta=5/x`, so
`theta=sin^-1(5/x)`
Vector Diagram (involving velocities):
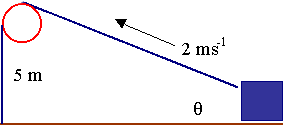
[See the section on Vector concepts for more on vectors and scalars.]
We are also given that:
`(dx)/(dt)=-2\ "ms"^-1`
Since we need `(d theta)/(dt)`, we use:
`(d theta)/(dt)=(d theta)/(dx)(dx)/(dt)`
Because
`theta=sin^-1(5/x)`
we have:
`(d theta)/(dx)=1/(sqrt(1-(5/x)^2))(d(5/x))/(dx)`
`=(-5)/(x^2sqrt(1-(5/x)^2))`
So
`(d theta)/(dt)=(d theta)/(dx)(dx)/(dt)`
`=(-5)/(x^2sqrt(1-(5/x)^2))(-2)`
`=10/(x^2sqrt(1-(5/x)^2))`
We want to know the rate of change of θ when x = 10 m, so we substitute, as follows:
`(d theta)/(dt)=10/(10^2sqrt(1-(5/10)^2))`
`=0.1155\ "rad"//"s"`
