2. Basic Principles of Counting
Later, on this page...
Counting
An efficient way of counting is necessary to handle large masses of statistical data (e.g. the level of inventory at the end of a given month, or the number of production runs on a given machine in a 24 hour period, etc.), and for an understanding of probability.
In this section, we shall develop a few counting techniques. Such techniques will enable us to count the following, without having to list all of the items:
- the number of ways,
- the number of samples, or
- the number of outcomes.
Before we learn some of the basic principles of counting, let's see some of the notation we'll need.
Number of Outcomes of an Event
As an example, we may have an event E defined as
E = "day of the week"
We write the "number of outcomes of event E" as n(E).
So in the example,
`n(E) = 7`,
since there are `7` days in the week.
Addition Rule
Let E1 and E2 be mutually exclusive events (i.e. there are no common outcomes).
Let event E describe the situation where either event E1 or event E2 will occur.
The number of times event E will occur can be given by the expression:
n(E) = n(E1) + n(E2)
where
n(E) = Number of outcomes of event E
n(E1) = Number of outcomes of event E1
n(E2) = Number of outcomes of event E2
[We see more on mutually exclusive events later in this chapter.]
Tip
In counting and probability, "OR" usually requires us to ADD.
Example 1
Consider a set of numbers `S = {-4, -2, 1, 3, 5, 6, 7, 8, 9, 10}`
Let the events E1, E2 and E3 be defined as:
E = choosing a negative or an odd number from S;
E1= choosing a negative number from S;
E2 = choosing an odd number from S.
Find n(E).
Answer
E1 and E2 are mutually exclusive events (i.e. no common outcomes).
n(E) = n(E1) + n(E2)
= 2 + 5
= 7
Example 2
In how many ways can a number be chosen from `1` to `22` such that
(a) it is a multiple of `3` or `8`?
(b) it is a multiple of `2` or `3`?
Answer
Part (a)
Here, E1 = multiples of `3`:
E1 = {3, 6, 9,12, 15, 18, 21}
n(E1) = 7
E2 = multiples of `8`:
E2 = {8, 16}
n(E2) = 2
Events E1 and E2 are mutually exclusive.
n(E) = n(E1) + n(E2) = 7 + 2 = 9
Part (b)
Here, E1 = multiples of `2`:
E1 = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22}
n(E1) = 11
E2 = multiples of `3`:
E2 = {3, 6, 9,12, 15, 18, 21}
n(E2) = 7
Events E1 and E2 are not mutually exclusive.
We could proceed as follows:
n(E) = n(E1) + n(E2) − n(E1 ∩ E2) = 11 + 7 − 3 = 15
where E1 ∩ E2 means "the intersection of the sets E1 and E2".
Multiplication Rule
Now consider the case when two events E1 and E2 are to be performed and the events E1 and E2 are independent events i.e. one does not affect the other's outcome.
[We see more on independent events later in this chapter.]
Example 3
Say the only clean clothes you've got are `2` t-shirts and `4` pairs of jeans. How many different combinations can you choose?
Answer
We can think of it as follows:
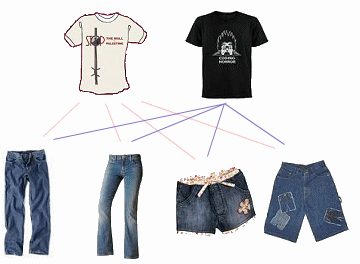
We have `2` t-shirts and with each t-shirt we could pick `4` pairs of jeans. Altogether there are
`2 × 4 = 8` possible combinations.
We could write
E1 = "choose t-shirt" and
E2 = "choose jeans"
Multiplication Rule in General
Suppose that event E1 can result in any one of n(E1) possible outcomes; and for each outcome of the event E1, there are n(E2) possible outcomes of event E2.
Together there will be n(E1) × n(E2) possible outcomes of the two events.
Tip
In counting and probability, "AND" usually requires us to MULTIPLY.
That is, if event E is the event that both E1 and E2 must occur, then
n(E) = n(E1) × n(E2)
In our example above,
n(E1) = 2 (since we had 2 t-shirts)
n(E2) = 4 (since there were 4 pairs of jeans)
So total number of possible outcomes is given by:
n(E) = n(E1) × n(E2) = 2 × 4 = 8
Example 4
What is the total number of possible outcomes when a pair of coins is tossed?
Answer
The events are described as:
E1 = toss first coin (2 outcomes, so n(E1) = 2.)
E2 = toss second coin (2 outcomes, so n(E2) = 2.)
They are independent, since neither toss affects the outcome of the other toss.
So n(E) = n(E1) × n(E2) = 2 × 2 = 4
[We could list the outcomes: HH HT TH TT].
Example 5
The life insurance policies of an insurance company are classified by:
- age of the insured:
- under 25 years,
- between 25 years and 50 years,
- over 50 years old;
- sex;
- marital status:
- single or
- married.
What is the total number of classifications?
Answer
The events are described as:
E1 = age of the insured: 3 age divisions, so n(E1) = 3.
E2 = sex: 2 possibilities, so n(E2) = 2.
E3 = marital status: 2 possibilities, so n(E3) = 2.
Each event is independent, so
n(E) = n(E1) × n(E2) × n(E3) = 3 × 2 × 2 = 12
Example 6
For our clothes problem above, say we found `3` caps that we could wear with our `2` t-shirts and `4` pairs of jeans. How many different combinations could we choose from now?
Answer
Our diagram now looks like this:
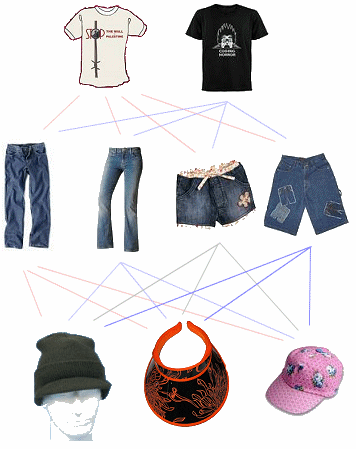
We have 2 choices in the first row, 4 in the second row and 3 in the third row. Together, we will have
n(E) = n(E1) × n(E2) = 2 × 4 × 3 = 24 combinations
Example 7

Image source: Monoface
In the excellent Monoface (external site, no longer available), we could change the head, left and right eyes, nose and mouth of some zany guys who work at momo-1.com.
We are told that there are 759,375 possible faces. Where does this number come from?
If they were to let us change the chin as well, how many possible combinations would there be?
Answer
There are `15` people in the photos (I got this by counting the number of heads) and there are `5` different options that you can change (head, left eye, right eye, nose and mouth).
So there are
`15 × 15 ×15 ×15 ×15` ` = 15^5` `= 759,375` combinations
If we add another possible event (changing the chin), we have `6` possible options, so the answer is simply:
`15^6= 11,390,625` combinations
