14. Normal Probability Distributions
On this page...
- Properties of a normal distribution
- Area under the normal curve
- Standard normal distribution
- Percentages of the area under standard normal curve
- The z-Table
- Application - stock market
Notation
We use upper case variables (like X and Z) to denote random variables, and lower-case letters (like x and z) to denote specific values of those variables.
The Normal Probability Distribution is very common in the field of statistics.
Whenever you measure things like people's height, weight, salary, opinions or votes, the graph of the results is very often a normal curve.
The Normal Distribution
A random variable X whose distribution has the shape of a normal curve is called a normal random variable.
This random variable X is said to be normally distributed with mean μ and standard deviation σ if its probability distribution is given by
`f(X)=1/(sigmasqrt(2pi))e^(-(x-mu)^2 "/"2\ sigma^2`
Properties of a Normal Distribution
-
The normal curve is symmetrical about the mean μ;
-
The mean is at the middle and divides the area into halves;
-
The total area under the curve is equal to 1;
-
It is completely determined by its mean and standard deviation σ (or variance σ2)
Note:
In a normal distribution, only 2 parameters are needed, namely μ and σ2.
Area Under the Normal Curve using Integration
The probability of a continuous normal variable X found in a particular interval [a, b] is the area under the curve bounded by `x = a` and `x = b` and is given by
`P(a<X<b)=int_a^bf(X)dx`
and the area depends upon the values of μ and σ.
[See Area under a Curve for more information on using integration to find areas under curves. Don't worry - we don't have to perform this integration - we'll use the computer to do it for us.]
The Standard Normal Distribution
It makes life a lot easier for us if we standardize our normal curve, with a mean of zero and a standard deviation of 1 unit.
If we have the standardized situation of μ = 0 and σ = 1, then we have:
`f(X)=1/(sqrt(2pi))e^(-x^2 "/"2`
We can transform all the observations of any normal random variable X with mean μ and variance σ to a new set of observations of another normal random variable Z with mean `0` and variance `1` using the following transformation:
`Z=(X-mu)/sigma`
We can see this in the following example.
Example 1
Say `μ = 2` and `sigma = 1/3` in a normal distribution.
The graph of the normal distribution is as follows:
The following graph (that we also saw earlier) represents the same information, but it has been standardized so that μ = 0 and σ = 1 (with the above graph superimposed for comparison):
The two graphs have different μ and σ, but have the same area.
The new distribution of the normal random variable Z with mean `0` and variance `1` (or standard deviation `1`) is called a standard normal distribution. Standardizing the distribution like this makes it much easier to calculate probabilities.
Formula for the Standardized Normal Distribution
If we have mean μ and standard deviation σ, then
`Z=(X-mu)/sigma`
Since all the values of X falling between x1 and x2 have corresponding Z values between z1 and z2, it means:
The area under the X curve between X = x1 and X = x2
equals
the area under the Z curve between Z = z1 and Z = z2.
Hence, we have the following equivalent probabilities:
P(x1 < X < x2) = P(z1 < Z < z2)
Example 2
Considering our example above where `μ = 2`, `σ = 1/3`, then
One-half standard deviation = `σ/2 = 1/6`, and
Two standard deviations = `2σ = 2/3`
So `1/2` s.d. (standard deviation) to 2 s.d. to the right of `μ = 2` will be represented by the area from `x_1=13/6 = 2 1/6 ~~ 2.167` to `x_2=8/3 = 2 2/3~~ 2.667`. This area is graphed as follows:
The area above is exactly the same as the area
z1 = 0.5 to z2 = 2
in the standard normal curve:
Percentages of the Area Under the Standard Normal Curve
A graph of this standardized (mean `0` and variance `1`) normal curve is shown.
In the above graph, we have indicated the areas between the regions as follows:
−1 ≤ Z ≤ 1 68.27%
−2 ≤ Z ≤ 2 95.45%
−3 ≤ Z ≤ 3 99.73%
This means that `68.27%` of the scores lie within `1` standard deviation of the mean.
This comes from: `int_-1^1 1/(sqrt(2pi))e^(-z^2 //2)dz=0.68269`
Also, `95.45%` of the scores lie within `2` standard deviations of the mean.
This comes from: `int_-2^2 1/(sqrt(2pi))e^(-z^2 //2)dz=0.95450`
Finally, `99.73%` of the scores lie within `3` standard deviations of the mean.
This comes from: `int_-3^3 1/(sqrt(2pi))e^(-z^2 //2)dz=0.9973`
The total area from `-∞ < z < ∞` is `1`.
The z-Table
The areas under the curve bounded by the ordinates z = 0 and any positive value of z are found in the z-Table. From this table the area under the standard normal curve between any two ordinates can be found by using the symmetry of the curve about z = 0. We can also use Scientific Notebook, as we shall see.
Go here for the actual z-Table.
Example 3
Find the area under the standard normal curve for the following, using the z-table. Sketch each one.
(a) between z = 0 and z = 0.78
(b) between z = −0.56 and z = 0
(c) between z = −0.43 and z = 0.78
(d) between z = 0.44 and z = 1.50
(e) to the right of z = −1.33.
Answer
From the z-table:
(a) Area = `0.2823`
(b) Area = `0.2123`
(c) Area = `0.1664 + 0.2823 = 0.4487`
(d) Area = `0.4332 - 0.1700 = 0.2632`
(e) Area = `0.4082 + 0.5 = 0.9082`
Example 4
Find the following probabilities:
(a) P(Z > 1.06)
(b) P(Z < -2.15)
(c) P(1.06 < Z < 4.00)
(d) P(-1.06 < Z < 4.00)
Answer
From the z-table:
(a)This is the same as asking "What is the area to the right of `1.06` under the standard normal curve?"
We need to take the whole of the right hand side (area `0.5`) and subtract the area from `z = 0` to `z = 1.06`, which we get from the z-table.
`P(Z >1.06)` `=0.5-P(0< Z<1.06)` `=0.5-0.355` `=0.1446`
(b)This is the same as asking "What is the area to the left of `-2.15` under the standard normal curve?"
This time, we need to take the area of the whole left side (`0.5`) and subtract the area from `z = 0` to `z = 2.15` (which is actually on the right side, but the z-table is assuming it is the right hand side.)
`P(Z <-2.15)` `=0.5-P(0< Z <2.15)` `=0.5-0.4842` `=0.0158`
(c) This is the same as asking "What is the area between `z=1.06` and `z=4.00` under the standard normal curve?"
`P(1.06< Z <4.00)`
`=P(0< Z <4.00)-` `P(0< Z <1.06)`
`=0.5-0.3554`
`=0.1446`
(d) This is the same as asking "What is the area between `z=-1.06` and `z=4.00` under the standard normal curve?"
We find the area on the left side from `z = -1.06` to `z = 0` (which is the same as the area from `z = 0` to `z = 1.06`), then add the area between `z = 0` to `z = 4.00` (on the right side):
`P(-1.06< Z <4.00)`
`=P(0< Z <1.06)+` `P(0< Z <4.00)`
`=0.3554+0.5`
`=0.8554`
Example 5
It was found that the mean length of `100` parts produced by a lathe was `20.05\ "mm"` with a standard deviation of `0.02\ "mm"`. Find the probability that a part selected at random would have a length
(a) between `20.03\ "mm"` and `20.08\ "mm"`
(b) between `20.06\ "mm"` and `20.07\ "mm"`
(c) less than `20.01\ "mm"`
(d) greater than `20.09\ "mm"`.
Answer
X = length of part
(a) `20.03` is `1` standard deviation below the mean;
`20.08` is `(20.08-20.05)/0.02=1.5` standard deviations above the mean.
`P(20.03 < X < 20.08)`
`=P(-1<Z<1.5)`
`=0.3413+0.4332`
`=0.7745`
So the probability is `0.7745`.
(b) `20.06` is `0.5` standard deviations above the mean;
`20.07` is `1` standard deviation above the mean
`P(20.06 < X < 20.07)`
`= P(0.5 < Z < 1)`
`=0.3413-0.1915`
`=0.1498`
So the probability is `0.1498`.
(c) `20.01` is `2` s.d. (standard deviations) below the mean.
`P(X<20.01)`
`=P(Z < -2)`
`=0.5-0.4792`
`=0.0228`
So the probability is `0.0228`.
(d) `20.09` is `2` s.d. above the mean, so the answer will be the same as (c),
`P(X > 20.09) = 0.0228.`
Example 6
A company pays its employees an average wage of `$3.25` an hour with a standard deviation of `60` cents. If the wages are approximately normally distributed, determine
- the proportion of the workers getting wages between `$2.75` and `$3.69` an hour;
- the minimum wage of the highest `5%`.
Answer
X = wage
(a) `Z_1=(2.75-3.25)/0.6=-0.83333 `
`Z_2=(3.69-3.25)/0.6=0.73333`
So
`P(2.75<X<3.69)`
`=P(-0.833<Z<0.733)`
`=0.298+0.268`
`=0.566`
So about `56.6%` of the workers have wages between `$2.75` and `$3.69` an hour.
You can see this portion illustrated in the standard normal curve below.
The normal curve with mean = 3.25 and standard deviation 0.60, showing the portion getting between $2.75 and $3.69.
(b) W = minimum wage of highest `5%`
`z = 1.645` (from table)
`(x-3.25)/0.6=1.645`
Solving gives: `x = 4.237`
So the minimum wage of the top `5%` of salaries is `$4.24`.
In the graph below, the yellow portion represents the 45% of the company's workers with salaries between the mean ($3.25) and $4.24. (This is 1.645 standard deviations from the mean.)
The light green shaded portion on the far right representats those in the top 5%.
The right-most portion represents those with salaries in the top 5%.
Example 7
The average life of a certain type of motor is `10` years, with a standard deviation of `2` years. If the manufacturer is willing to replace only `3%` of the motors because of failures, how long a guarantee should she offer? Assume that the lives of the motors follow a normal distribution.
Answer
X = life of motor
x = guarantee period
We need to find the value (in years) that will give us the bottom 3% of the distribution. These are the motors that we are willing to replace under the guarantee.
`P(X < x) = 0.03`
The area that we can find from the z-table is
`0.5 - 0.03 = 0.47`
The corresponding z-score is `z = -1.88`.
Since `Z=(x-mu)/sigma`, we can write:
`(x-10)/2=-1.88`
Solving this gives `x = 6.24.`
So the guarantee period should be `6.24` years.
Here's a graph of our situation. Our normal curve has μ = 10, σ = 2.
The yellow portion represents the 47% of all motors that we found in the z-table (that is, between 0 and −1.88 standard deviations).
The light green portion on the far left is the 3% of motors that we expect to fail within the first 6.24 years.
The left-most portion represents the 3% of motors that we are willing to replace.
Application - The Stock Market
Sometimes, stock markets follow an uptrend (or downtrend) within `2` standard deviations of the mean. This is called moving within the linear regression channel.
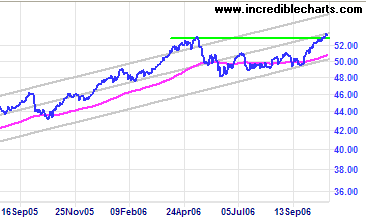
Here is a chart of the Australian index (the All Ordinaries) from 2003 to Sep 2006.
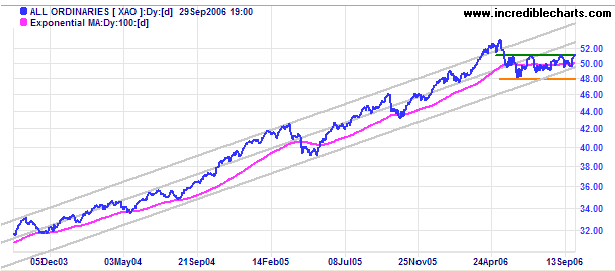
Image source: incrediblecharts.com.
The upper gray line is `2` standard deviations above the mean and the lower gray line is `2` standard deviations below the mean.
Notice in April 2006 that the index went above the upper edge of the channel and a correction followed (the market dropped).
But interestingly, the latter part of the chart shows that the index only went down as far as the bottom of the channel and then recovered to the mean, as you can see in the zoomed view below. Such analysis helps traders make money (or not lose money) when investing.
Image source: incrediblecharts.com.