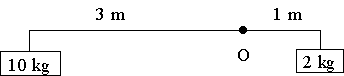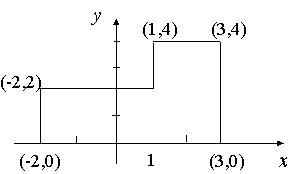5. Centroid of an Area by Integration
by M. Bourne
Typical (straight sided) Problem
In tilt-slab construction, we have a concrete wall (with doors and windows cut out) which we need to raise into position. We don't want the wall to crack as we raise it, so we need to know the center of mass of the wall. How do we find the center of mass for such an uneven shape?

Tilt-slab construction (aka tilt-wall or tilt-up)
In this section we'll see how to find the centroid of an area with straight sides, then we'll extend the concept to areas with curved sides where we'll use integration.
Moment
The moment of a mass is a measure of its tendency to rotate about a point. Clearly, the greater the mass (and the greater the distance from the point), the greater will be the tendency to rotate.
The moment is defined as:
Moment = mass × distance from a point
Example 1
In this case, there will be a total moment about O of:
(Clockwise is regarded as positive in this work.)
`M = 2 × 1 − 10 × 3 = -28\ "kgm"`
Centre of Mass
We now aim to find the centre of mass of the system and this will lead to a more general result.
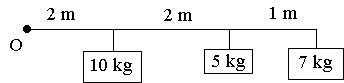
Example 2
We have 3 masses of 10 kg, 5 kg and 7 kg at 2 m, 2 m and 1 m distance from O as shown.
We wish to replace these masses with one single mass to give an equivalent moment. Where should we place this single mass?
Answer
Total moment `= 10 × 2 + 5 × 4 + 7 × 5 = 75\ "kg.m"`
If we put the masses together, we have: `10 + 5 + 7 = 22\ "kg"`
For an equivalent moment, we need:
`22 times bar(d)=75`
where `bar(d)` is the distance from the center of mass to the point of rotation.
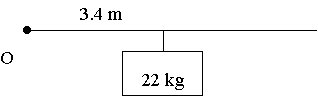
i.e. `bar(d)=75/22 approx 3.4\ text[m]`
So our equivalent system (with one mass of `22\ "kg"`) would have:
Centre of Mass (Centroid) for a Thin Plate
1) Rectangle:
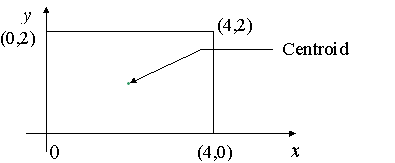
The centroid is (obviously) going to be exactly in the centre of the plate, at (2, 1).
2) More Complex Shapes:
We divide the complex shape into rectangles and find `bar(x)` (the x-coordinate of the centroid) and `bar(y)` (the y-coordinate of the centroid) by taking moments about the y- and x-coordinates respectively.
Because they are thin plates with a uniform density, we can just calculate moments using the area.
Example 3
Find the centroid of the shape:
Answer
We divide the area into 2 rectangles and assume the mass of each rectangle is concentrated at the center.
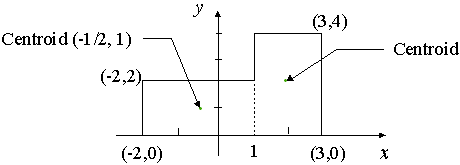
Left rectangle: `"Area" = 3 × 2 = 6\ "sq unit"`. Center `(-1/2, 1)`
Right rectangle: `"Area" = 2 × 4 = 8\ "sq unit"`. Center `(2, 2)`
Taking moments with respect to the y-axis, we have:
`6(- 1/2)+8(2)=(6+8)barx`
`-3+16=14 barx`
`barx = 13/14`
Now, w.r.t the x-axis:
`6(1)+8(2)=(6+8)bary`
`6+16=14bary`
`bary=22/14`
`=1 4/7`
So the centroid is at: `(13/14, 1 4/7)`
We would use this process to solve the tilt slab construction problem mentioned at the beginning of this section.
In general, we can say:
`bar(x)=("total moments in"\ x"-direction")/"total area"`
`bar(y)=("total moments in"\ y"-direction")/"total area"`
This idea is used more extensively in the next section.
Centroid for Curved Areas
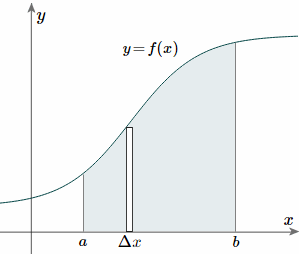
Taking the simple case first, we aim to find the centroid for the area defined by a function f(x), and the vertical lines x = a and x = b as indicated in the following figure.
To find the centroid, we use the same basic idea that we were using for the straight-sided case above. The "typical" rectangle indicated is `x` units from the `y`-axis, and it has width `Δx` (which becomes `dx` when we integrate) and height y = f(x).
Generalizing from the above rectangular areas case, we multiply these 3 values (`x`, `f(x)` and `Deltax`, which will give us the area of each thin rectangle times its distance from the `x`-axis), then add them. If we do this for infinitesimally small strips, we get the `x`-coordinates of the centroid using the total moments in the x-direction, given by:
`bar(x)="total moments"/"total area"` `=1/Aint_a^b x\ f(x)\ dx`
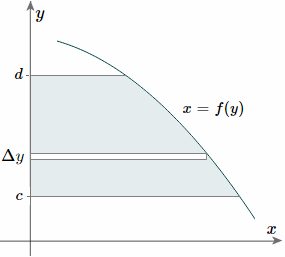
And, considering the moments in the y-direction about the x-axis and re-expressing the function in terms of y, we have:
`bar(y)="total moments"/"total area"` `=1/Aint_c^d y\ f(y)\ dy`
Notice this time the integration is with respect to `y`, and the distance of the "typical" rectangle from the `x`-axis is `y` units. Also note the lower and upper limits of the integral are `c` and `d`, which are on the `y`-axis.
Of course, there may be rectangular portions we need to consider separately. (I've used a different curve for the `bary` case for simplification.)
Alternate method: Depending on the function, it may be easier to use the following alternative formula for the y-coordinate, which is derived from considering moments in the x-direction (Note the "dx" in the integral, and the upper and lower limits are along the x-axis for this alternate method).
`bar(y)="total moments"/"total area"`
`=1/Aint_a^b f(x)/2 xx f(x) dx`
`=1/Aint_a^b ([f(x)]^2)/2 dx`
This is true since for our thin strip (width `dx`), the centroid will be half the distance from the top to the bottom of the strip.
Another advantage of this second formula is there is no need to re-express the function in terms of y.
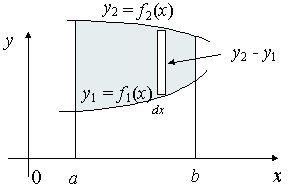
Centroids for Areas Bounded by 2 Curves
We extend the simple case given above. The "typical" rectangle indicated has width Δx and height y2 − y1, so the total moments in the x-direction over the total area is given by:
`bar(x)="total moments"/"total area"` `=1/Aint_a^b x\ (y_2-y_1)\ dx`
For the y coordinate, we have 2 different ways we can go about it.
Method 1: We take moments about the y-axis and so we'll need to re-express the expressions x2 and x1 as functions of y.
`bar(y)="total moments"/"total area"` `=1/Aint_c^d y\ (x_2-x_1)\ dy`
Method 2: We can also keep everything in terms of x by extending the "Alternate Method" given above:
`bar(y)="total moments"/"total area"` `=1/Aint_a^b ([y_2]^2-[y_1]^2)/2 dx`
Example 4
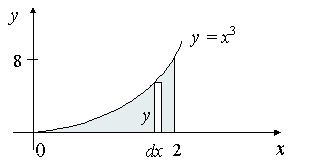
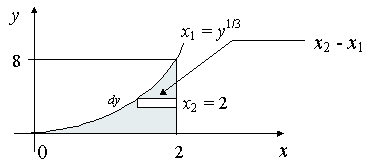
Find the centroid of the area bounded by y = x3, x = 2 and the x-axis.
Answer
Here is the area under consideration:
In this case, `y = f(x) = x^3`, `a = 0`, `b = 2`.
We find the shaded area first:
`A=int_0^2 x^3 dx = [(x^4)/(4)]_0^2=16/4=4`
Next, using the formula for the x-coordinate of the centroid we have:
`barx=1/A int_a^b xf(x) dx`
`=1/4 int_0^2 x(x^3) dx`
`=1/4 int_0^2 (x^4) dx`
`=1/4[(x^5)/(5)]_0^2`
`=32/20`
`=1.6`
Now, for the y coordinate, we need to find:
`x_2 = 2` (this is fixed in this problem)
`x_1 = y^(1//3)` (this is variable in this problem)
`c = 0`, `d = 8`.`bary=1/A int_c^d y(x_2-x_1) dy`
`=1/4 int_0^8 y(2-y^[1/3]) dy`
`=1/4 int_0^8(2y - y^[4/3]) dy`
`=1/4[y^2-(3y^[7/3])/(7)]_0^8`
`=1/4 [64-(3 times 128)/(7)]`
`=2.29`
So the centroid for the shaded area is at (1.6, 2.29).
Alternate Method for the y-coordinate
Using the "Method 2" formula given, we could also obtain the y-coordinate of the centroid as follows:
`bary=1/A int_a^b ([f(x)]^2)/(2) dx`
`=1/4 int_0^2 ([x^3]^2)/(2) dx`
`=1/4 int_0^2 (x^6)/(2) dx`
`=1/56 [x^7]_0^2`
`=2.29`
In this example, Method 2 is easier than Method 1, but it may not always be the case.