6. Expressing a sin θ ± b cos θ in the form R sin(θ ± α)
by M. Bourne
In electronics, we often get expressions involving the sum of sine and cosine terms. It is more convenient to write such expressions using one single term.
Our Problem:
Express a sin θ ± b cos θ in the form
R sin(θ ± α),
where a, b, R and α are positive constants.
Solution:
First we take the "plus" case, (θ + α), to make things easy.
Let
a sin θ + b cos θ ≡ R sin (θ + α)
(The symbol " ≡ " means: "is identically equal to")
Using the compound angle formula from before (Sine of the sum of angles),
sin(A + B) = sin A cos B + cos A sin B,
we can expand R sin (θ + α) as follows:
R sin (θ + α)
≡ R (sin θ cos α + cos θ sin α)
≡ R sin θ cos α + R cos θ sin α
So
a sin θ + b cos θ ≡ R cos α sin θ + R sin α cos θ
Equating the coefficients of sin θ and cos θ in this identity, we have:
For sin θ:
a = R cos α ..........(1)
(in green above)
For cos θ:
b = R sin α .........(2)
(in red above)
Eq. (2) ÷ Eq.(1):
`b/a=(R sin alpha)/(R cos alpha)=tan alpha`
So
`alpha=arctan\ b/a`
(α is a positive acute angle and a and b are positive.)
Now we square each of Eq. (1) and Eq. (2) and add them to find an expression for R.
[Eq. (1)]2 + [Eq. (2)]2:
a2 + b2
= R2 cos2 α + R2 sin2 α
= R2(cos2 α + sin2 α)
= R2
(since cos2 A + sin2 A = 1)
So
`R=sqrt(a^2+b^2`
(We take only the positive root)
In summary, if
`alpha=arctan\ b/a`
and
`R=sqrt(a^2+b^2)`
then we have expressed a sin θ + b cos θ in the form required:
a sin θ + b cos θ = R sin(θ + α)
You will notice that this is very similar to converting rectangular to polar form in Polar form of Complex Numbers. We can get α and R using calculator, similar to the way we did it in the complex numbers section.
The Minus Case
Similarly, for the minus case, we equate a sin θ − b cos θ with the expansion of R sin (θ − α) as follows (note the minus signs carefully):
a sin θ − b cos θ ≡ R cos α sin θ − R sin α cos θ
Once again we will obtain (try it yourself!):
`alpha=arctan\ b/a`
and
`R=sqrt(a^2+b^2)`
Our equation for the minus case is:
a sin θ − b cos θ = R sin(θ − α)
Equations of the type a sin θ ± b cos θ = c
To solve an equation in the form
a sin θ ± b cos θ = c,
express the LHS in the form R sin(θ ± α) and then solve
R sin(θ ± α) = c.
Exercises - Sine Form
1. (a) Express 4 sin θ + 3 cos θ in the form R sin(θ + α).
(b) Using your answer from part (a), solve the equation
4 sin θ + 3 cos θ = 2 for 0° ≤ θ < 360°.
Answer
Part (a)
Firstly, let:
4 sin θ + 3 cos θ ≡ R sin(θ + α)
Then we need:
`R=sqrt(4^2+3^2)=sqrt25=5`
`alpha=arctan(3/4)=36.87^@`
So
4 sin θ + 3 cos θ = 5 sin(θ + 36.87°)
What have we done?
The components of the original function were:
(i) 4 sin θ (in black)
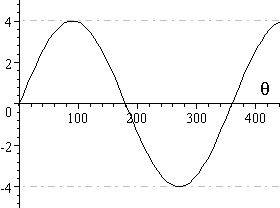
(ii) 3 cos θ (in blue, with 4 sin θ)
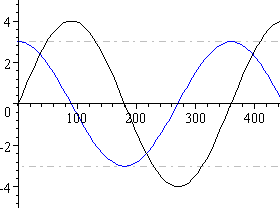
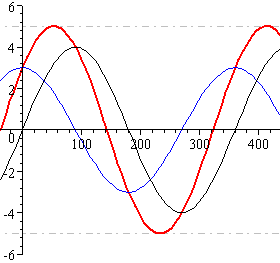
When we add these 2 components we get a sine curve that has been shifted to the left by `36.87^@`:
4 sin θ + 3 cos θ = 5 sin(θ + 36.87°) (in red)
Part (b)
From part (a),
4 sin θ + 3 cos θ = 5 sin(θ + 36.87°)
So,
5 sin(θ + 36.87°) = 2
sin(θ + 36.87°) = 0.4
Sine is positive in Quadrants I and II.
Solving sin α = 0.4, we get the reference angle α = 23.58°.
So the angle for Quadrant I is 23.58° and for Quadrant II, is 180° − 23.58° = 156.42°.
So, we get
`theta+36.87^@=23.58^@`
OR
`theta+36.87^@=156.42^@`
And this gives us:
`theta=23.58^@-36.87^@`
`=-13.29^@`
`=346.71^@`
OR
`theta=156.42^@-36.87^@`
`=119.55^@`
Are these answers correct?
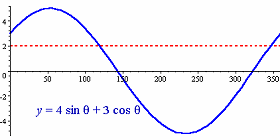
We can see from the graph that in the domain 0° ≤ θ < 360°, the only two angles which give a value of 2 are 119.6° and 346.7°. So our answer is correct.
2. Solve the equation
`sin theta-sqrt2 cos theta=0.8`, for 0° ≤ θ < 360°.
Answer
Firstly, express the LHS in the form R sin(θ − α) (Note the negative sign!):
`sin theta-sqrt2 cos theta` ≡ `R sin(theta-alpha)`
`R=sqrt(1^2+(sqrt2)^2)=` `sqrt(1+2)=` `sqrt3`
`alpha=arctan(sqrt2/1)=54.74^@`
So
`sin theta-sqrt2\ cos theta` ≡ `sqrt3\ sin(theta-54.74^@)`
Now, solving the original equation gives:
`sqrt3\ sin(theta-54.74^@)=0.8`
`sin(theta-54.74^@)=0.8/sqrt3=0.4619`
Sine is positive in Quadrants I and II.
So, from calculator, we get
`theta-54.74^@=27.51^@`
OR
`theta-54.74^@=152.49^@`
And this gives us:
`theta=27.51^@+54.74^@=82.25^@`
OR
`theta=152.49^@+54.74^@=207.23^@`
Are these answers correct?
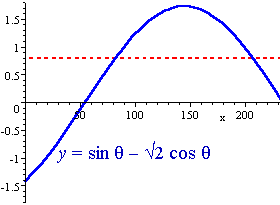
We can see from the graph that in the domain `0^@ ≤ θ < 360^@`, the only two angles which give a value of 0.8 (the red dotted line) are `82.3^@` and `207.2^@`. So our answer is correct.
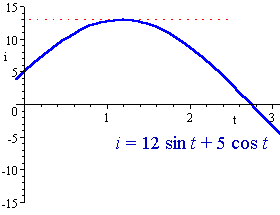
3. The current i (in amperes) at time t in a particular circuit is given by
i = 12 sin t + 5 cos t.
Find the maximum current and the first time that it occurs.
Answer
Note that normally we take t ≥ 0. For this sort of example, we must use radians for the angle.
We have:
`R=sqrt(12^2+5^2)=13` and `alpha=arctan(5/12)=0.39479`.
So `12\ sin t+5\ cos t=` `13\ sin(t+0.39479)`
So we can see that the amplitude is 13 A and this is the maximum value.
To find the first time that it occurs, we need to solve
`13\ sin(t+0.39479)=13`
That is
`sin(t+0.39479)=1`
Now sin θ = 1 for the first time when `theta=pi/2`. So we need to solve:
`t+0.39479=pi/2`
`t=pi/2-0.39479=1.176`
So the maximum value of 13 A will first occur at time t = 1.176 s.
We can see that this is correct from the graph:
`i=12\ sin t+5\ cos t`
4. Solve 7 sin 3θ − 6 cos 3θ = 3.8 for 0° ≤ θ < 360°.
Answer
Firstly, express the LHS in the form R sin(3θ − α).
(Note the negative sign and the `3θ`! We have to increase the domain by 3 times.)
`7\ sin 3theta-6\ cos 3theta` ≡ `R\ sin(3theta-alpha)`
`R=sqrt(7^2+6^2)` `=sqrt(49+36)=sqrt85`
`alpha=arctan(6/7)=40.60^@`
So
`7\ sin 3theta-6\ cos 3theta` ≡ `sqrt85sin(3theta-40.60^@)`
Now, solving the original equation gives:
`sqrt85sin(3theta-40.60^@)` `=3.8`
` sin(3theta-40.60^@)` `=3.8/sqrt85` `=0.412`
Since we have 3θ , we must use the domain: `0^@ ≤ 3θ < 1080^@`.
Sine is positive in Quadrants I,II and V, VI and IX and X.
So, from our calculator, we get the following for `(3θ − 40.60^@)`:
`24.33^@, 155.67^@, 384.33^@,` `515.67^@, 744.33^@ and 875.67^@`
So `3θ` will be:
`64.93^@, 196.27^@, 424.93^@,` `556.27^@, 784.93^@, 916.27^@`.
So the solutions for `θ` are:
`21.6^@, 65.4^@, 141.6^@,` `185.4^@, 261.6^@, 305.4^@`.
5. The current i amperes in a certain circuit after t seconds is given by
`i=2\ sin(t-pi/3)-cos(t+pi/2)`
Find the maximum current and the earliest time it occurs.
(Note: t > 0)
Answer
We need to get this in a simpler form. In this one, notice that the angles in the brackets are not the same!
We must simplify them first so the angles in the brackets are the same.
`i=2\ sin(t-pi/3)-cos(t+pi/2)`
`=2(sin t cos {:pi/3:}-cos t sin {:pi/3:} )` `-(cos t cos {:pi/2:} - sin t sin {:pi/2:})`
`=2((sin t)/2-0.866\ cos t)` `-(cos txx0-sin t xx1)`
`=sin t-1.732\ cos t+sin t`
`=2\ sin t-1.732\ cos t`
Now we can express i in the form R sin(t + α).
`R=sqrt(2^2+1.732^2)=2.646`
`alpha=arctan(1.732/2)=` `0.714\ text(radians`
So
`2\ sin t − 1.732\ cos t =` ` 2.646\ sin(t − 0.714)`
So the maximum value of this is `2.646\ "A"`.
To find when this occurs, we need to solve:
`2.646\ sin(t − 0.714) = 2.646`
i.e. `sin(t − 0.714) = 1`
`t − 0.714 = π/2``t = 2.29`
So `t = 2.29\ "s"` is the time when the maximum is first reached.
The Cosine Form
We can also express our sum of a sine term and a cosine term using cosine rather than sine. It may be more convenient to do so in some situations.
The expressions obtained are similar to those we obtained for the sine case, but note the differences as we proceed.
For a, b and R positive and α acute, our equivalent expression is given by:
a sin θ + b cos θ ≡ R cos (θ − α)
This time there is a difference in the way we obtain α, compared to before.
Expanding R cos (θ − α) using our result for the expansion of cos(A − B) gives us:
R cos (θ − α) = R cos θ cos α + R sin θ sin α
Rearranging and equating co-efficients gives us
a sin θ + b cos θ ≡ R cos α cos θ + R sin α sin θ
So:
a = R sin α ..... (1)
b = R cos α ..... (2)
Dividing (1) by (2) gives us:
`a/b=(R sin alpha)/(R cos alpha)=tan alpha`
Therefore:
`alpha=arctan\ a/b`
(Note the fraction is `a/b` for the `"cosine"` case, whereas it is `b/a` for the `"sine"` case.)
We find R the same as before:
`R=sqrt(a^2+b^2)`
So the sum of a sine term and cosine term have been combined into a single cosine term:
a sin θ + b cos θ ≡ R cos(θ − α)
Once again, a, b, R and α are positive
constants and α is acute.
The Cosine Minus Case
If we have a sin θ − b cos θ and we need to express it in terms of a single cosine function, the formula we need to use is:
a sin θ − b cos θ ≡ −R cos (θ + α)
Once again, a, b and R are positive.
`α` is acute and given by:
`alpha=arctan\ a/b`
R is given by:
`R=sqrt(a^2+b^2`
Cosine Exercises
1. Express 7 sin θ + 12 cos θ in the form R cos (θ − α), where 0 ≤ α < π/2.
Answer
We find α using
`alpha=arctan\ a/b`
α has to be in radians for this example, since we are told `0 ≤ α < π/2`.
Since `a = 7` and `b = 12`, we have:
`α = arctan (7/12) = 0.528`
We find R using
`R=sqrt(a^2+b^2`
So `R=sqrt(7^2+12^2)=13.892`
Therefore we can write:
7 sin θ + 12 cos θ = 13.892 cos (θ − 0.528)
To check our answer, we draw the graphs of both y = 7 sin θ + 12 cos θ and y = 13.892 cos (θ − 0.528). We see that they are exactly the same. (Only one is shown).
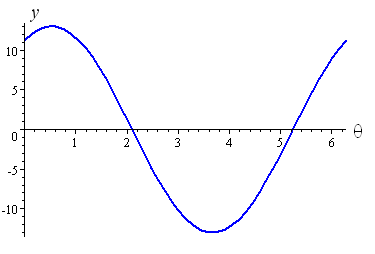
We observe that our cosine graph has amplitude `13.892` and it has been shifted to the right by `0.528` radians, which is consistent with the expression we obtained: 13.892 cos (θ − 0.528)
2. Express 2.348 sin θ − 1.251 cos θ in the form −R cos (θ + α), where 0 ≤ α < π/2.
Answer
We find α using
`a=text(arctan)a/b`
Once again, `α` has to be in radians for this example.
Since `a = 2.348` and `b = 1.251`, we have:
`α = arctan (2.348/1.251) = 1.081 `
We find R using
`R=sqrt(a^2+b^2)`
So `R=sqrt(2.348^2+ 1.251^2) = 2.660`
So we can write:
2.340 sin θ − 1.251 cos θ = -2.660 cos (θ + 1.081)
Checking using a graph, we obtain the following for each side of our answer:
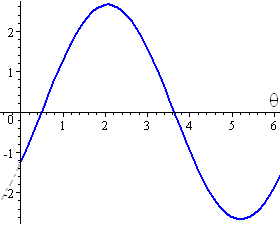
We see that our negative cosine curve has an amplitude of 2.660 and it has been shifted to the left by 1.081 radians, which is consistent with the expression −2.660 cos (θ + 1.081).
Summary
Here is a summary of the expressions and conditions that we have found in this section.
| Original Expression | Combined Expression | α |
|---|---|---|
| a sin θ + b cos θ | R sin (θ + α) | `alpha=` `arctan (b/a)` |
| a sin θ − b cos θ | R sin (θ − α) | `alpha=` `arctan (b/a)` |
| a sin θ + b cos θ | R cos (θ − α) | `alpha=` `arctan (a/b)` |
| a sin θ − b cos θ | −R cos (θ + α) | `alpha=` `arctan (a/b)` |
In each case, a, b and R are positive and α is an acute angle.
R is given by:
`R=sqrt(a^2+b^2)`
