2. Sin, Cos and Tan of Sum and Difference of Two Angles
by M. Bourne
The sine of the sum and difference of two angles is as follows:
On this page...
sin(α + β) = sin α cos β + cos α sin β
sin(α − β) = sin α cos β − cos α sin β
The cosine of the sum and difference of two angles is as follows:
cos(α + β) = cos α cos β − sin α sin β
cos(α − β) = cos α cos β + sin α sin β
Proofs of the Sine and Cosine of the Sums and Differences of Two Angles
We can prove these identities in a variety of ways.
Here is a relatively simple proof using the unit circle:
Proof 1
Proof 1 - Using the Unit Circle
We start with a unit circle (which means it has radius 1), with center O.
We construct angles `BOA = alpha` and `AOP = beta` as shown.
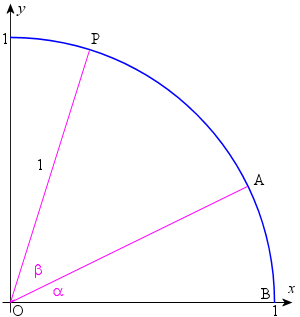
Next, we drop a perpendicular from P to the x-axis at T. Point C is the intersection of OA and PT.
We then construct line PR perpendicular to OA.
Finally, we drop a perpendicular from R to the x-axis at S, and another from R to PT at Q, as shown.
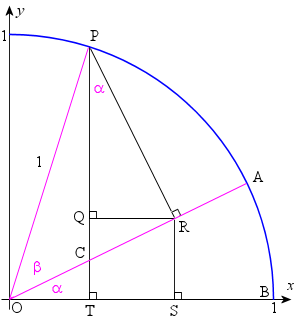
We note the following:
(1) `/_TPR = alpha` since triangles OTC and PRC are similar. (`/_OTC = /_PRC = 90°`, and `/_OCT = /_PCR = 90°- alpha`.)
(2) Length |QT| = |RS|
(3) sin (α + β) = |PT| = |PQ| + |QT| = |PQ| + |RS|
(4) |PR| = sin (β)
(5) In triangle PQR, |PQ| = |PR| cos (α)
(6) So from (4) and (5), |PQ| = sin (β) cos (α).
(7) |OR| = cos (β)
(8) In triangle OSR, |RS| = |OR| sin (α)
(9) So from (7) and (8), |RS| = cos (β) sin (α)
(10) Thus from (3), (6) and (9), we have proved:
sin (α + β) = sin (β) cos (α) + cos (β) sin (α)
Rearranging gives:
sin (α + β) = sin (α) cos (β) + cos (α) sin (β)
(11) From Even and Odd Functions, we have: cos (−β) = cos( β) and sin (−β) = −sin(β)
(12) So replacing β with (−β), the identity in (10) becomes
sin (α − β) = sin α cos β − cos α sin β
[Thank you to David McIntosh for providing the outline of the above proof.]
The Cosine Proofs
We now need to prove
cos (α + β) = cos α cos β − sin α sin β
(13) |OT| = cos (α + β)
(14) In triangle ORS, we have: `cos alpha = |OS|/|OR|`.
(15) cos (β) = |OR|, from (7) above.
(16) From (14) and (15), we obtain `cos alpha cos beta= |OS|/|OR|xx|OR| = |OS|`.
(17) In triangle QPR, we have `sin alpha = |QR|/|PR|`.
(18) sin (β) = |PR|, from (4) above.
(19) From (17) and (18), we obtain `sin alpha sin beta= |QR|/|PR|xx|PR| = |QR|`.
(20) Now |OS| − |QR| = |OT|.
(21) So `cos alpha cos beta - sin alpha sin beta` ` = cos(alpha+beta)`.
(22) Rearranging, we have:
cos (α + β) = cos α cos β − sin α sin β
(23) Once again, we replace β with (−β), and the identity in (22) becomes:
cos (α − β) = cos α cos β + sin α sin β
The next proof is the standard one that you see in most text books. It also uses the unit circle, but is not as straightforward as the first proof. However, we can still learn a lot from this next proof, especially about the way trigonometric identities work.
Proof 2
Proof 2 - Using the Unit Circle
We will prove the cosine of the sum of two angles identity first, and then show that this result can be extended to all the other identities given.
cos (α+β) = cos α cos β − sin α sin β
We draw a circle with radius 1 unit, with point P on the circumference at (1, 0).
We draw an angle α from the centre with terminal point Q at (cos α, sin α), as shown. [Q is (cos α, sin α) because the hypotenuse is 1 unit.]
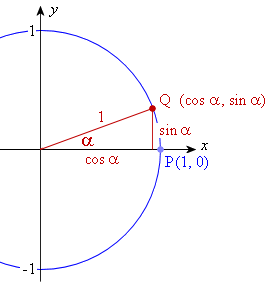
We extend this idea by drawing:
a. The angle β with terminal points at Q (cos α, sin α) and R (cos (α + β), sin (α + β))
b. The angle −β with terminal point at S (cos (−β), sin (−β))
c. The lines PR and QS, which are equivalent in length.
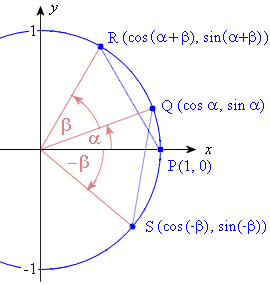
Now, using the distance formula from Analytical Geometry, we have:
PR2 = (cos (α + β) − 1)2 + sin2(α + β)
= cos2(α + β) − 2 cos (α + β) + 1 + sin2(α + β)
= 2 − 2cos (α + β)
[since sin2(α + β) + cos2(α + β) = 1]
Now using the distance formula on distance QS:
QS2 = (cos α − cos (−β))2 + (sin α − sin (−β))2
= cos2 α − 2 cos α cos(−β) + cos2(−β) + sin 2α − 2sin α sin(−β) + sin2(−β)
= 2 − 2cos α cos(−β) − 2sin α sin(−β)
[since
sin2α + cos2α = 1 and
sin2(−β) + cos2(−β) = 1]
= 2 − 2cos α cos β + 2sin α sin β
[since
cos(−β) = cos β (cosine is an even function) and
sin(−β) = −sinβ (sine is an odd function − see Even and Odd Functions)]
Since PR = QS, we can equate the 2 distances we just found:
2 − 2cos (α + β) = 2 − 2cos α cos β + 2sin α sin β
Subtracting 2 from both sides and dividing throughout by −2, we obtain:
cos (α + β) = cos α cos β − sin α sin β
If we replace β with (−β), this identity becomes:
cos (α − β) = cos α cos β + sin α sin β
[since cos(−β) = cos β and sin(−β) = −sinβ]
Sine of the Sum of Two Angles
We aim to prove that
sin (α + β) = sin α cos β + cos α sin β
Recall that (see phase shift)
sin (θ) = cos (π/2− θ)
If θ = α + β, then we have:
sin (α + β)
= cos [π/2 − (α + β)]
= cos [π/2 − α − β)]
Next, we re-group the angles inside the cosine term, since we need this for the rest of the proof:
cos [π/2 − α − β)] = cos [(π/2 − α) − β]
Using the cosine of the difference of 2 angles identity that we just found above [which said
cos (α − β) = cos α cos β + sin α sin β],
we have:
cos [(π/2 − α) − β]
= cos (π/2 − α) cos (β) + sin (π/2 − α) sin (β)
= sin α cos β + cos α sin β
[Since cos (π/2 − α) = sin α; and sin (π/2 − α) = cos α]
Therefore:
sin (α + β) = sin α cos β + cos α sin β
Replacing β with (−β), this identity becomes (because of Even and Odd Functions):
sin (α − β) = sin α cos β − cos α sin β
We have proved the 4 identities involving sine and cosine of the sum and difference of two angles.
Summary:
sin (α + β) = sin α cos β + cos α sin β
sin (α − β) = sin α cos β − cos α sin β
cos (α+β) = cos α cos β − sin α sin β
cos (α − β) = cos α cos β + sin α sin β
Finally, here is an easier proof of the identities, using complex numbers:
Proof 3
Proof 3 - Using Complex Numbers
The exponential and polar forms of a complex number provide an easy way to prove the fundamental trigonometric identities.
Assume we have 2 complex numbers which we write as:
r1ejα = r1(cos α + j sin α)
and
r2ejβ = r2(cos β + j sin β)
We multiply these complex numbers together.
Multiplying the left hand sides:
r1ejα × r2ejβ = r1r2ej(α+β)
We can write this answer as:
r1r2ej(α+β) = r1r2(cos (α+β) + j sin (α+β)) ... (1)
Multiplying the right hand sides:
r1(cos α + j sin α) × r2(cos β + j sin β)
= r1 r2(cos α cos β + j cos α sin β + j sin α cos β − sin α sin β)
= r1 r2(cos α cos β − sin α sin β + j (cos α sin β + sin α cos β)) .... (2)
[since j2 = −1]
Now, equating (1) and (2) and dividing both parts by r1 r2:
cos (α+β) + j sin (α+β) = cos α cos β − sin α sin β + j (cos α sin β + sin α cos β)
Equating the real parts gives:
cos (α+β) = cos α cos β − sin α sin β
Equating the imaginary parts gives:
sin (α+β) = sin α cos β + cos α sin β
We would then proceed to replace β with (−β) as before, to obtain the identities for sin (α − β) and cos (α − β).
Tangent of the Sum and Difference of Two Angles
We have the following identities for the tangent of the sum and difference of two angles:
`tan(alpha+beta)=(tan alpha+tan beta)/(1-tan alpha\ tan beta)`
and
`tan(alpha-beta)=(tan alpha-tan beta)/(1+tan alpha\ tan beta)`
Proof of the Tangent of the Sum and Difference of Two Angles
Our proof for these uses the trigonometric identity for tan that we met before.
Proof
Case: `tan(alpha+beta)`
Recall that
`tan theta=(sin theta)/(cos theta)`
So, letting θ = α + β, and expanding using our new sine and cosine identities, we have:
`tan(alpha+beta)` `=(sin(alpha+beta))/(cos(alpha+beta))` `=(sin alpha cos beta+cos alpha sin beta)/(cos alpha cos beta-sin alpha sin beta)`
Dividing numerator and denominator by cos α cos β:
`=(sin alpha cos beta+cos alpha sin beta)/(cos alpha cos beta-sin alpha sin beta)` `-:(cos alpha cos beta)/(cos alpha cos beta`
Simplifying gives us:
`tan(alpha+beta)=` `(tan alpha+tan beta)/(1-tan alpha\ tan beta)`
Case: `tan(alpha-beta)`
Replacing β with (−β) gives us
`tan(alpha-beta)=` `(tan alpha-tan beta)/(1+tan alpha\ tan beta)`
[The tangent function is odd, so tan(−β) = − tan β]
We have proved the two tangent of the sum and difference of two angles identities:
`tan(alpha+beta)=` `(tan alpha+tan beta)/(1-tan alpha\ tan beta)`
`tan(alpha-beta)=` `(tan alpha-tan beta)/(1+tan alpha\ tan beta)`
Example 1
Find the exact value of cos 75o by using 75o = 30o + 45o.
Answer
Recall the 30-60 and 45-45 triangles from Values of Trigonometric Functions:
We use the exact sine and cosine ratios from the triangles to answer the question as follows:
`cos 75^"o"=cos(30^("o")+45^("o"))`
`=cos 30^("o")\ cos 45^("o")-sin 30^("o")\ sin 45^("o")`
`=sqrt3/2(1)/sqrt2-1/2(1)/sqrt2`
`=(sqrt3-1)/(2sqrt2)`
This is the exact value for cos 75o.
Example 2
If `sin α = 4/5` (in Quadrant I) and `cos β = -12/13` (in Quadrant II) evaluate `sin(α − β).`
Answer
We use
sin(α − β) = sin α cos β − cos α sin β
We firstly need to find `cos α` and `sin β`.
If `sin α = 4/5`, then we can draw a triangle and find the value of the unknown side using Pythagoras' Theorem (in this case, 3):
We do the same thing for `cos β = 12/13`, and we obtain the following triangle.
Note 1: We are using the positive value `12/13` to calculate the required reference angle relating to `beta`.
Note 2: The sine ratio is positive in both Quadrant I and Quadrant II.
Note 3: We have used Pythagoras' Theorem to find the unknown side, 5.
Now for the unknown ratios in the question:
`cos α = 3/5 `
(positive because in quadrant I)
`sin β = 5/13`(positive because in quadrant II)
We are now ready to find the required value, sin(α − β):
`sin(alpha-beta)=` `sin alpha\ cos beta-cos alpha\ sin beta`
`=4/5(-12/13)-3/5(5/13)`
`=(-48-15)/65`
`=(-63)/65`
This is the exact value for sin(α − β).
Exercises
1. Find the exact value of cos 15o by using 15o = 60o − 45o
Answer
Once again, we use the 30o-60o and 45o-45o triangles to find the exact value.
`cos 15^("o")=cos(60^("o")-45^("o"))`
`=cos 60^("o") cos 45^("o") +\ sin 60^("o") sin 45^("o")`
`=1/2(1)/sqrt2+sqrt3/2(1)/sqrt2`
`=(1+sqrt3)/(2sqrt2)`
2. If `sin α = 4/5` (in Quadrant I) and `cos β = -12/13` (in Quadrant II) evaluate `cos(β − α).`
[This is not the same as Example 2 above. This time we need to find the cosine of the difference.]
Answer
In this case, for the cosine of the difference of two angles, we have:
`cos(beta-alpha)=` `cos beta cos alpha+sin beta sin alpha`
`=((-12)/13)3/5+(5/13)4/5`
`=(-36+20)/65`
`=(-16)/65`
3. Reduce the following to a single term. Do not expand.
cos(x + y)cos y + sin(x + y)sin y
Answer
We recognise this expression as the right hand side of:
cos(α − β) = cos α cos β + cos α cos β,
with α = x + y and β = y.
We can now write this in terms of cos(α − β) as follows:
cos(x + y)cos y + sin(x + y)sin y
= cos[(x + y) − (y)]
= cos x
We have reduced the expression to a single term.
4. Prove that
`cos(30^"o"+x)=(sqrt3 cos x-sin x)/2`
Answer
We recall the 30-60 triangle from before (in Values of Trigonometric Functions):
Using
cos(α + β) = cos α cos β − sin α sin β
and our 30-60 triangle, we start with the left hand side (LHS) and obtain:
`"LHS"=cos(30^"o"+x)`
`=cos 30^"o"\ cos x - sin 30^"o"\ sin x`
`=sqrt3/2 cos x-1/2sin x`
`=(sqrt3\ cos x-sin x)/2`
`="RHS"`
Since the LHS = RHS, we have proved the identity.
