6. Superannuation

by M. Bourne

Superannuation is just a fancy word which means "savings for retirement".

In the past, you would pay taxes all your life and then expect the government to look after you until you died, by giving you a government pension. This didn’t cost much for governments because they knew you would not live very long and there were not so many old people around. They were getting lots of tax from the large number of working baby-boomers (those born from 1945 to 1960), so they could afford to pay for pensions.

However, the situation has changed. Now the baby-boomers are approaching retirement and they are expected to live a lot longer and the proportion of young working people has dropped.

So it means we all have to save for our own retirement. We can’t expect governments to bail us out - they will go broke.

Saving for Retirement

Most governments provide generous tax arrangements for retirement savings. The idea is that you put some money into a superannuation fund each month and let it grow. You leave it there until you retire around age 60 and then take the money out each month via an annuity. When you buy an annuity, you are buying a constant income stream for a certain length of time (either a fixed time period or for the rest of your life.) Let’s see how this works in an example.

Scenario

Tom (see the Chapter Introduction) is now 35 and he wants to retire at age 55. He believes he can live on $36000 per year once he has finished working.

He decides to save like mad now so that he can meet his goal.

Let’s assume that his superannuation fund will earn 5% per year. This is a reasonable expectation. We’ll assume that Tom buys a 20-year annuity and that the 5% rate is in force until Tom reaches 75 years of age. (Actually, this is very unlikely. Interest rates are constantly going up and down. But for the sake of this example, we’ll assume an overall increase of 5% per year.)

So he will be saving for 20 years and then withdrawing the money at $3000 per month for 20 years.

Value of the Annuity - Growth Phase

In the first 20 years, Tom feels that he can afford to pay `$1000` per month into the retirement fund. Will it be enough?

The formula for the value of an increasing annuity is given by

`V=P((1+r)^n-1)/r`

where

V = value of the annuity

P = the amount we pay each period

r = interest (or earning) rate, p.a., expressed as a decimal

n = the number of periods that we have been paying into the annuity.

Since Tom is paying monthly, we have to tweak this formula a little, and divide the earnings rate by 12.

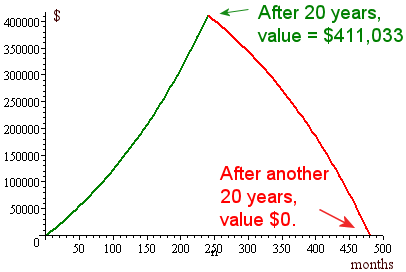
The value of Tom’s annuity after 20 years is:

`V=1000((1+0.05/12)^(20xx12)-1)/(0.05/12)` `=411033.72`

Not bad - $1000 per month for 20 years and he has just over $411,000.

Value of the Annuity - Withdrawal Phase

So Tom retires at age 55 and now starts to draw on the money. He wants `$3000` per month. To find the amount remaining at the end of the 20 years retirement period, we need to remember that the `$411033.72` principle is decreasing by the amount Tom takes out each month, and then interest is earned on − and added to − what remains.

The balance of the annuity at time period n is given by:

`B=P(1+r)^n-W((1+r)^n-1)/r`

where

B is the balance at time period n

P is the principal amount we start with

W is the amount we want to take out each time period

r is the interest rate p.a. expressed as a decimal

n is the time period

(This is similar to a mortgage that we saw before.)

So in Tom’s case, if he takes `$3000` out each month, the amount remaining after 20 years will be:

`411033.72(1+0.05/12)^(20xx12)` `-3000((1+0.05/12)^(20xx12)-1)/(0.05/12) ` `=-118114.44`

This is not good - it is negative so Tom has run out of money before he turns 75! He has been taking too much out each month. Now he realises he will have to live on less than $3000 per month.

How much can he take out each month? The formula we use is:

`text(Payment)=(Vr)/(1-(1+r)^-n)`

where

V is the amount we start with

r is the interest rate p.a. expressed as a decimal

n is the time period

So Tom will be able to take out:

`text(Payment)=(411033.72xx0.05/12)/(1-(1+0.05/12)^(-20xx12))` `=$2712.64`

Not bad - not quite `$3000` per month but it’s almost there. Notice how a small sacrifice makes a big difference.

Let’s see how that looks on a chart.

Other Scenarios

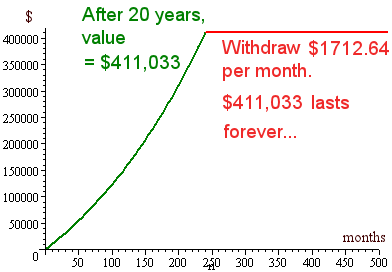
1. Tom realises that he may live a lot longer than 75. Also, he wants to leave some money to his children after he goes over to the Other Side. How much can he take out per month so that the $411,033 does not diminish?

Answer

In this case, we want the balance to be the same as the amount we start with. So we solve the balance equation above as follows:

`B=P(1+r)^n-W((1+r)^n-1)/r`

`411033.72` `=411033.72(1+0.05/12)^(20xx12)` `-W((1+0.05/12)^(20xx12)-1)/(0.05/12)`

Solving for W:

The first expression on the right hand side has value 1114986.717.

Adding the W part to both sides and subtracting 411033.72 from both sides gives:

`W((1+0.05/12)^(20xx12)-1)/(0.05/12)` `=1114986.717-411033.72` `=703952.997`

This gives us:

`W=((0.05/12)703952.997)/((1+0.05/12)^(20xx12)-1)=1712.64`

So the amount we can take out each month such that the $411,033 lasts forever is:

`W = $1712.64`

The graph for this situation is as follows:

Of course, don’t forget the importance of inflation. His $411,033 will decrease in value (spending power) as time goes on.

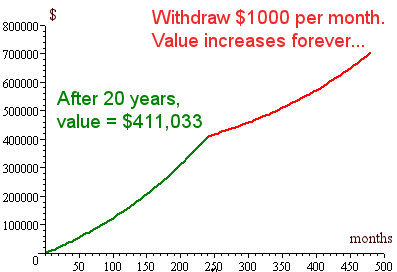
2. For interest, let’s see what happens when Tom takes out the same amount that he puts in. That is, he withdraws $1000 per month. Once again, the money lasts forever and continues to increase in value. Cool, huh? This is the power of compounding.

Financial Lessons From All This

• Tom (see the chapter intro) should learn as much as he can about superannuation and understand the power of compounding.
• Tom should learn as much as he can about investing - and start doing it - while he is still young.

Money Maths Lesson Plan Suggestions - Superannuation

Simulate a scenario where students have different amounts to invest each month. They need to find current interest rates and invest for different periods of time. Then they need to choose a retirement age and figure out what they can withdraw from their savings and for how long. What are the risks in annuities?

Footnote

Inflation is an important consideration in all financial planning. Think about the effect of inflation on the above scenarios.